5. Винтовые поверхности

Винтовой поверхностью называется поверхность образованная винтовым движением образующей вокруг винтовой оси і. Линейчатая винтовая поверхность, в определитель которой входит цилиндрическая винтовая линия (гелиса), называется геликоидом. Если образующая перпендикулярна к винтовой оси, то геликоид называется ......................... . В противном случае он называется .................. или ................................ .

Пример 9. Построить очерк поверхности косого геликоида β(i,[AB],|P|), где i(i1,i2)-ось, (AB)-образующая, |P|-шаг винтовой поверхности. Определить фрон-тальную проекцию точки N(N2), принадлежащую этой поверхности. Решение: P

B1 A1 B2=i2 A2 N2 i1

Лабораторная работа №9.

ИЗУЧЕНИЕ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ПЛОСКОСТЬЮ, ПРЯМОЙ И ДРУГОЙ ПОВЕРХНОСТЬЮ

ПОСТРОЕНИЕ РАЗВЕРТОК ПОВЕРХНОСТЕЙ

(5 часов)

Цель лабораторной работы: изучение способов построения линии пересечения поверхностей; изучение способов построения разверток поверхностей.

1. Пересечение поверхностей

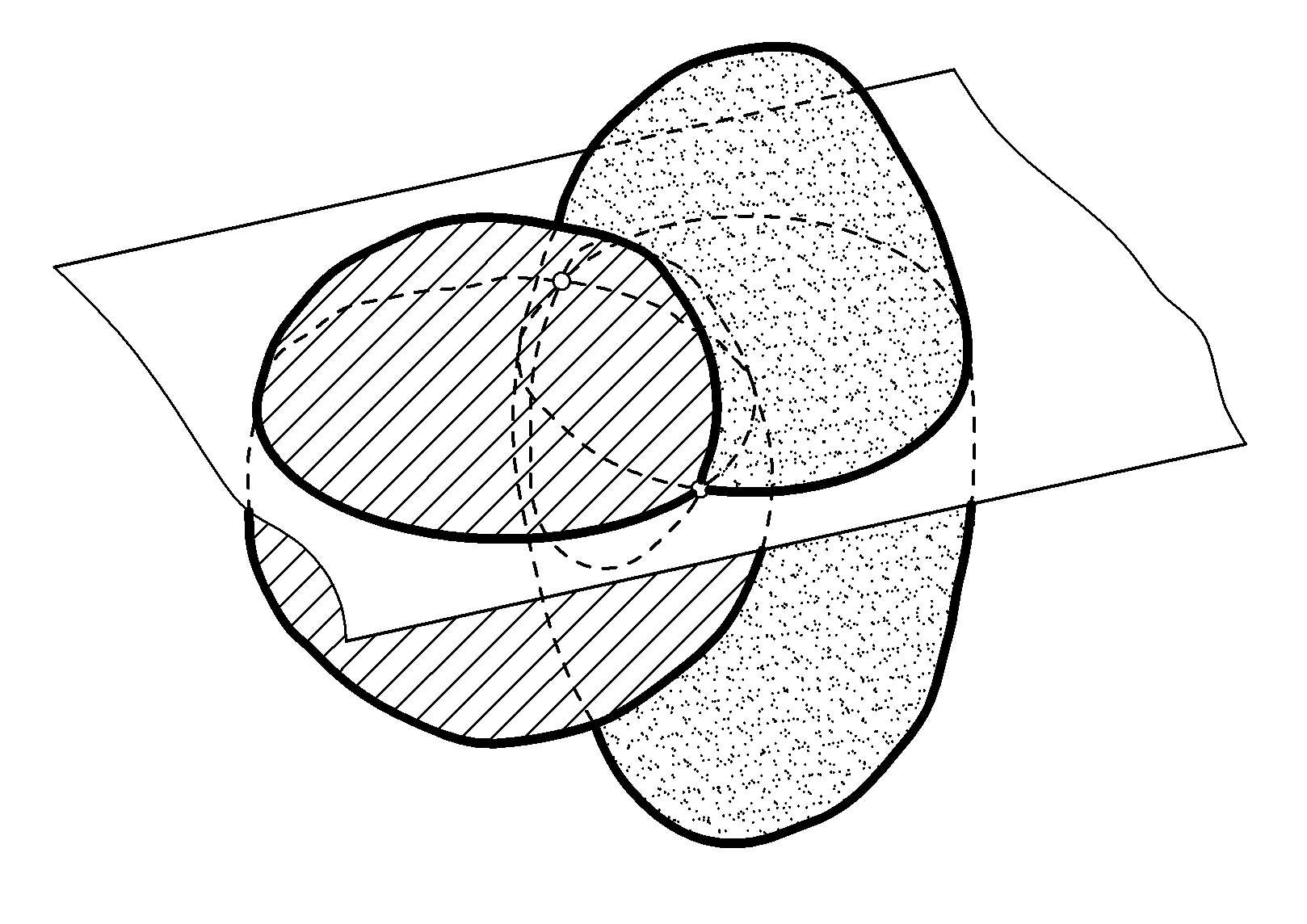
Линия пересечения двух поверхностей определяется по точкам. Алгоритм определения точки К, принадлежащей поверхностям α и β:

1) рассечем заданные поверхности дополнительной поверхностью γ^і ;

2) построим линии пересече-ния поверхности γі с поверхност-ями (α и β) - это линии (аі и bi); 3) найдем точку пересечения (К і) (аі и bi). Эта точка будет принадлежать линии пересечения заданных поверхностей; 4) аналогично, используя се-мейство дополнительных секущих поверхностей, определим ряд точек; 5) соединим построенные точки плавной кривой.

bi ai α β k Ki γ i . .

i=1,2,…n	Дано: поверхность α и β Определить: α∩β=k? Алгоритм: Р ассечь заданные поверхности поверхностью γ і γ і ∩ α=a i; γ і ∩ β=b i; a i ∩ b i=К і; . .. ... ... ...
	3n+1. соединим построенные точки К і плавной кривой.

В качестве дополнительных секущих поверхностей применяют плоскости, сферы и другие поверхности.

Секущие поверхности подбирают так, чтобы они рассекали заданные поверхности по наиболее простым для построения линиям - прямым или окружностям.