- •II часть. Практика. Алгебра логики.
- •1. Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему):
- •2. Укажите, какие из высказываний предыдущего упражнения истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
- •3. Сформулируйте отрицания следующих высказываний:
- •4. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет:
- •5. Формализуйте следующий вывод: "Если a и b истинны, то c — истинно. Но c — ложно: значит, a или b ложны".
- •7. Из двух данных высказываний a и b постройте составное высказывание, которое было бы:
- •8. Определите с помощью таблиц истинности, какие из следующих формул являются тождественно истинными или тождественно ложными:
- •9. Упростите следующие формулы, используя законы склеивания:
- •10. Упростите следующие формулы, используя законы поглощения:
- •11. Постройте таблицы истинности для логических формул и упростите формулы, используя законы алгебры логики:
- •14. Приведите примеры истинных и ложных высказываний:
5. Формализуйте следующий вывод: "Если a и b истинны, то c — истинно. Но c — ложно: значит, a или b ложны".
(((a b) => c) ^ с) =>(˅)
6. Пусть a = “это утро ясное”, а b = “это утро теплое”. Выразите следующие формулы на обычном языке:
а) “это утро ясное и тёплое”;
ж) “это утро не ясное или не тёплое”;
б) “это утро ясное и оно не тёплое”;
з) “это утро не ясное и не тёплое”;
в) “это утро не ясное и оно не тёплое”;
и) “это утро ясное или не тёплое”;
г) “это утро не ясное или оно тёплое”;
к) “если это тро ясное, то оно не тёплое”;
д) “это утро ясное или оно не тёплое”;
л) “если это утро не ясное, то оно тёплое”;
е) “это утро не ясное или оно не тёплое”;
м) “это утро ясное и не тёплое”.
7. Из двух данных высказываний a и b постройте составное высказывание, которое было бы:
а) истинно тогда и только тогда, когда оба данных выказывания ложны;
б) ложно тогда и только тогда, когда оба данных высказывания истинны.
а) не а * не б
б) не а + не б
8. Определите с помощью таблиц истинности, какие из следующих формул являются тождественно истинными или тождественно ложными:
а) |
д) |
б) |
е) |
в) |
ж) |
г) |
|
Истинные:
а)
Переменные |
Промежуточные логические формулы |
Формула |
||||||||
a |
b |
|
·a |
|
a·b |
a·b ˅ b |
b · (a·b ˅ b) |
|
||
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
||
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
||
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
||
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||
в)
Переменные |
Промежуточные логические формулы |
Формула |
|||||
a |
b |
|
|
a·b |
˅ |
|
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
е)
Переменные |
Промежуточные логические формулы |
Формула |
||||||||||
a |
b |
c |
|
|
˅b |
˅c |
˅c |
( ˅b)·( ˅c) |
( ˅b)·( ˅c) |
|
||
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
||
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
||
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
||
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
||
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
||
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
||
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
||
Ложные:
г)
Переменные |
Промежуточные логические формулы |
Формула |
|||||||||
a |
b |
c |
d |
e |
|
|
a·b |
c˅ ˅d |
·( c˅ ˅d) |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
д)
Переменные |
Промежуточные логические формулы |
Формула |
||||
a |
b |
|
|
˅ |
b·( ˅ ) |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
ж)
Переменные |
Промежуточные логические формулы |
Формула |
|||||
a |
b |
|
|
a=>b |
=> |
(a=>b)( => ) |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |

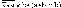
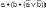
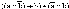
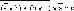
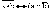


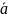
 ·a
·a