1.2.7. Похідна за напрямом. Градієнт

Означення. Нехай функція визначена в деякому околі точки ; l — деякий промінь з початком у точці ; — точка на цьому промені, яка належить околу точки (рис. 1.23); — довжина відрізка . Якщо існує

,

то ця границя називається похідною функції за напрямом l у точці і позначається .

Зокрема, — похідна функції за додатним напрямом осі х, а — похідна функції за додатним напрямом осі у.

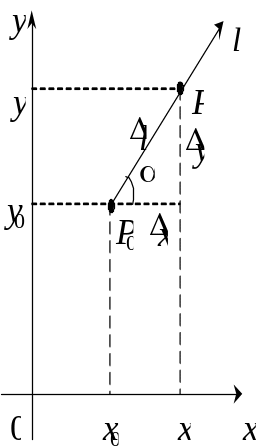
Рис. 1.23

Похідна за напрямом характеризує швидкість зміни функції у точці за напрямом l.

Теорема 1.18. Якщо функція має в точці неперервні частинні похідні, то в цій точці існує похідна за будь-яким напрямом , причому

(12)

де і — значення частинних похідних у точці .

З найти похідну функції у точці за напрямом

^● Знайдемо та обчислимо частинні похідні в точці функції :

Тоді за формулою (12) маємо:

.

Означення. Вектор з координатами , який характеризує напрям максимального зростання функції в точ­ці , називається градієнтом функції у цій точці і позначається :

(13)

де i, j — одиничні орти.

З найти градієнт функції у точці .

^● Запишемо та обчислимо частинні похідні в точці :

;

Тоді згідно з (13) , або .

Аналогічно для диференційовної функції у точці похідна за напрямом довільного одинично­го вектора , подається так:

Означення. Градієнтом диференційовної функції у точці називають вектор де — одиничні орти, а значення частинних по- хідних обчислені в точці .

Властивості:

1. .

2. .

3. Якщо , то похідна досягає найбільшого значення при .

1.2.8. Частинні похідні і повні диференціали вищих порядків

Нехай функція має частинні похідні в усіх точках множини D. Візьмемо будь-яку точку . Якщо в цій точці існують частинні похідні і , то вони залежать від х і у, тобто вони є функціями двох змінних. Отже, можна ставити питання про відшукання їх частинних похідних. Якщо вони існують, їх називають частинними похідними другого порядку і позначають відповідно (читаємо: «де два зет по де ікс квадрат») або , або , або , або Аналогічно визначаються і позначаються частинні похідні третього і вищих порядків.

Нехай функція в околі точки має частинну похідну першого порядку .

Означення. Частинну похідну функції за змінною називають частинною похідною другого порядку за змінними і і позначають або

Отже, за означенням:

.

Якщо , похідну позначають .

Означення. Частинною похідною порядку називають частинну похідну першого порядку за будь-якою змінною від будь-якої похідної порядку.

Частинні похідні за різними змінними називають мішаними частинними похідними.

Теорема 1.19. Якщо дві мішані похідні порядку m, що відріз­няються лише порядком диференціювання, неперервні в деякій точці, то їх значення в цій точці збігаються.

З найти , якщо .

^● Маємо:

З найти і для функції .

^● .

Означення. Диференціалом другого порядку функції називається диференціал її повного диференціала:

.

Аналогічно визначаються диференціали третього і вищих порядків:

.

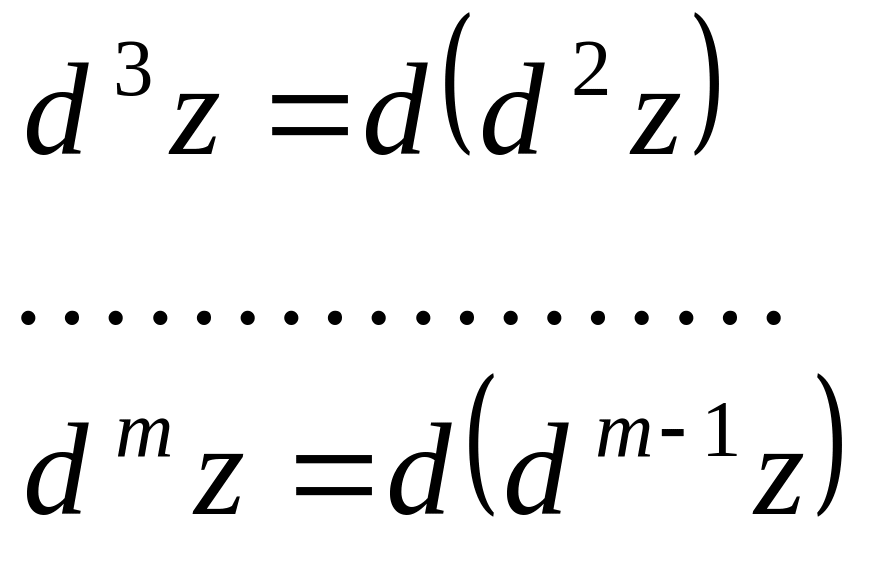Для диференціала порядку m справджується залежність:

(14)

У частинному випадку при формула (14) набирає вигляду:

(15)

З ауваження. Для складеної функції , де , , другий її диференціал, загалом, не подається через dx і dy згідно з формулою (15). Отже, для порядку не виконується властивість інваріантності форми диференціала щодо вибору змінних.

У разі функції n змінних формула (14) набирає вигляду:

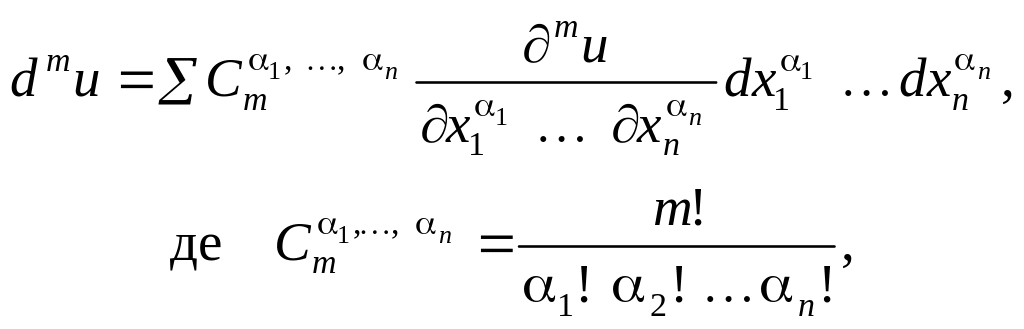(16)

де підсумовування виконується за всіма цілими невід’ємними , такими що .

При формула (16) подається так:

Знайти , якщо

^● , ;

, ; .

Згідно з (15) маємо: