Навчальні завдання
Приклад.
У
просторі R
дано множину
.
Вказати внутрішні, межові точки множини
Е
у просторі R.
(0, 1) — усі точки інтервалу внутрішні; x = 0, x = 1, x = 2 — межові точки.
Приклад.
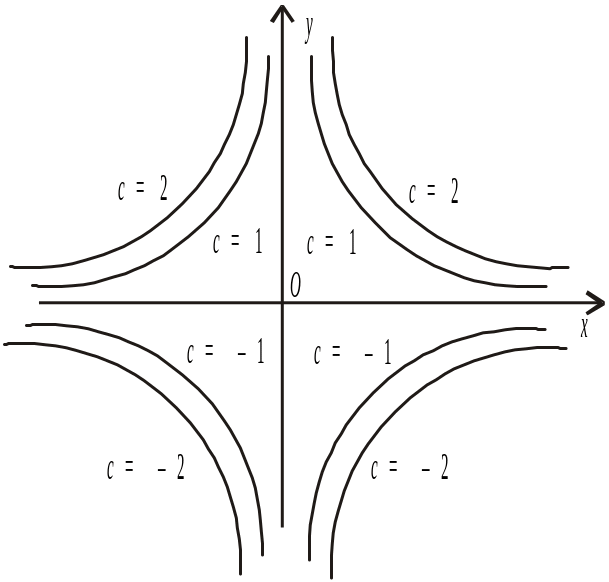
Побудувати
лінії рівня функції
.
Рівняння
ліній рівня має вигляд
або
.
Узявши
,
дістанемо сім’ю ліній рівня (рис. 1.13).
|
|
Рис. 1.13 |
Рис. 1.14 |
Приклад. Знайти область визначення функції двох змінних та надати їй геометричну інтерпретацію:
а) 
;
б) 
;
в) 
;
г) 
.
а) Функція
невизначена, якщо
.
Геометрично це означає, що область
визначення складається із двох
напівплощин,
одна з яких лежить вище,
а друга — нижче від прямої
(рис. 1.14).
б) Функція
визначена, якщо
,
тобто
.
Це є коло з центром (0; 0) та радіусом 1
(рис. 5.15).
в) Функція
визначена, якщо
,
тобто
(рис. 5.16).
г) Функція
визначена, якщо
,
тобто
(рис. 5.17).
|
|
|
Рис. 1.15 |
Рис. 1.16 |
Рис. 1.17 |
Приклад.
Знайти границю функції
.
Для
будь-якого
існує
(наприклад,
)
таке, що для всіх точок
,
що задовольняють умову
і відрізняються від початку координат,
виконується нерівність
.
Отже,
.
Приклад. Знайти точки розриву функції двох змінних:
1) 
;
2) 
.
1.
Функція
у точці x
= 0, y
= 0 не існує, тому вона має в цій точці
розрив. Знайдемо границю
.
Для
будь-якого
існує
,
що для всіх точок
,
що задовольняють умову
і відрізняються від початку координат,
виконується нерівність:
.
Отже,
і функція має в точці (0; 0) розрив.
2. Функція
не існує, якщо
,
тобто
.
Тому може бути, що вона має розрив.
Знайдемо границю
.
Отже, функція має в точці (0; 0) розрив.
Завдання для перевірки знань
1. Встановити, чи є множина Е в просторі R3 а) зв’язною; б) відкритою; в) областю:
1) 
;
2) 
;
3) 
.
Відповідь. 1. а) так, б) так, в) так;
2. а) так, б) ні, в) ні;
3. а) ні, б) так, в) ні.
2. Знайти та зобразити область визначення функції двох змінних:
1) 
; 2) 
;
3) 
; 4) 
;
5) 
; 6)
;
7)
; 8)
;
9)
; 10)
;
11)
;
12)
.
9. Знайти область визначення функції двох змінних
і встановити, чи буде вона неперервною в області визначення.
10. Знайти всі точки розриву функції:
1) 
; 3) 
;
2) 
; 4) 
.
5)
; 6)
.
Тема 1.2 Диференційовність функції двох змінних
1.2.1. Частинні та повний прирости функції двох змінних
Нехай
функція
визначена в деякому околі точки
.
Надамо незалежним змінним x
та y
приросту відповідно
та
так, щоб точка
не виходила за межі вказаного околу.
Тоді й точки
,
також належатимуть розглядуваному
околу (рис. 1.18).
Рис. 1.18
Означення.
Різницю
називають
повним приростом
функції
при переході від точки
до точки
і позначають
.
Різницю
називають частинним
приростом за х,
а різницю
— частинним
приростом за y
функції
;
їх позначають відповідно
і
.
Таким чином,
,
,
.
Зауваження. Аналогічно визначаються прирости функції більш ніж двох змінних.