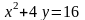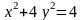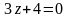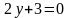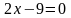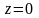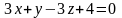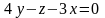- •Методические указания
- •Введение
- •Методические указания к расчетно-графическим работам
- •Варианты контрольных заданий. Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 23
- •Вариант 24
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Тестовые задания по темам: «Элементы линейной алгебры», «Элементы аналитической геометрии», «Элементы векторной алгебры».
- •Список рекомендованной литературы
Вариант 26
1. Решить системы линейных уравнений двумя способами: а) методом Крамера и с помощью обратной матрицы; б) методом Гаусса.
а)
б)

2. Даны координаты вершины пирамиды А1А2А3А4 :
А1(0; -2;2), А2(5;-2;2), А3(1;4;3), А4(2; 2;6). Найти:
1) длину ребраА1А2; 2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3; 4) объем пирамиды;
5) уравнение прямой А1А2; 6) уравнение плоскости А1А2А3.
Сделать чертеж.
3. Построить на плоскости область решений системы неравенств

Вариант 27
1. Решить системы линейных уравнений двумя способами: а) методом Крамера и с помощью обратной матрицы; б) методом Гаусса.
а)
б)

2. Даны координаты вершины пирамиды А1А2А3А4 :
А1(3; 1;5), А2(3;7;5), А3(2;1;4), А4(9; 4;7). Найти:
1) длину ребраА1А2; 2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3; 4) объем пирамиды;
5) уравнение прямой А1А2; 6) уравнение плоскости А1А2А3.
Сделать чертеж.
3. Построить на плоскости область решений системы неравенств

Вариант 28
1. Решить системы линейных уравнений двумя способами: а) методом Крамера и с помощью обратной матрицы; б) методом Гаусса.
а)
б)

2. Даны координаты вершины пирамиды А1А2А3А4 :
А1(-3; 2;0), А2(0;2;-4), А3(2;1;1), А4(-4; 4;-2). Найти:
1) длину ребраА1А2; 2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3; 4) объем пирамиды;
5) уравнение прямой А1А2; 6) уравнение плоскости А1А2А3;
Сделать чертеж.
3. Построить на плоскости область решений системы неравенств
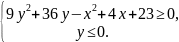
Вариант 29
1. Решить системы линейных уравнений двумя способами: а) методом Крамера и с помощью обратной матрицы; б) методом Гаусса.
а)
б)
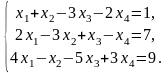
2. Даны координаты вершины пирамиды А1А2А3А4 :
А1(6; 2;4), А2(2;0;8), А3(6;3;1), А4(12; -1;6). Найти:
1) длину ребраА1А2; 2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3; 4) объем пирамиды;
5) уравнение прямой А1А2; 6) уравнение плоскости А1А2А3.
Сделать чертеж.
3. Построить на плоскости область решений системы неравенств

Вариант 30
1. Решить системы линейных уравнений двумя способами: а) методом Крамера и с помощью обратной матрицы; б) методом Гаусса.
а)
б)

2. Даны координаты вершины пирамиды А1А2А3А4 :
А1(0; 1;-5), А2(3;5;-5), А3(2;2;-3), А4(2; -1;-4). Найти:
1) длину ребраА1А2; 2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3; 4) объем пирамиды;
5) уравнение прямой А1А2; 6) уравнение плоскости А1А2А3.
Сделать чертеж.
3. Построить на плоскости область решений системы неравенств

Тестовые задания по темам: «Элементы линейной алгебры», «Элементы аналитической геометрии», «Элементы векторной алгебры».
Определитель
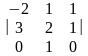 равен…
равен…
1)-1 2) 1 3) 5 4) -5
Если
 и
и
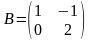 ,
то матрица С=2А+В
имеет вид…
,
то матрица С=2А+В
имеет вид…
1)
 2)
2)
 3)
4)
3)
4)

Матрица
 вырождена при λ, равном …
вырождена при λ, равном …
1)2 2) 3 3) 8/3 4) -8/3
В система уравнений
 независимыми
(свободными) переменными можно считать…
независимыми
(свободными) переменными можно считать…
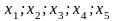 2)
2)
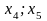 3)
3)
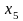 4)
4)
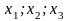
Даны точки А(2;3) и В(-6;5), тогда координаты середины отрезка АВ равны…
(-4;1) 2) (-2;4) 3) (-4;8) 4) (-2;8)
Прямая проходит через точки О(0;0) и В(-2;1), тогда ее угловой коэффициент равен…
2 2) ½ 3) -2 4) -1/2
Нормальный вектор плоскости
 имеет
координаты…
имеет
координаты…
(1;-4;-8) 2) (1;-4;8) 3) (-4;-8;-3) 4) (1;-4;-3)
Установите соответствие между уравнением плоскости и ее положением в пространстве:
1)
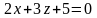
2)

3)
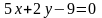
4)
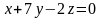
А) параллельна оси у; Б) параллельна оси х;
В) проходит через начало координат; Г)параллельна оси z;
Д) проходит через ось у.
Разложение определителя
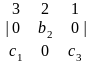 по элементам второй строки имеет вид
…
по элементам второй строки имеет вид
…
1)
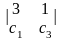 2)
2)
 3)
3)
 4)
4)
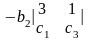
Если
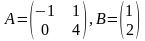 ,
тогда матрица С=А∙В
имеет вид…
,
тогда матрица С=А∙В
имеет вид…
1)
 2)
2)
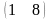 3)
3)
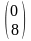 4)
4)
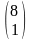
Ранг матрицы
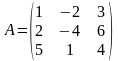 равен…
равен…
1) 2 2) 3 3) 0 4) 1
Если (х0,у0) – решение системы линейных уравнений
 ,
то х0
может определяться по формуле…
,
то х0
может определяться по формуле…
1)
 2)
2)
 3)
3)
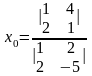 4)
4)

Если уравнение гиперболы имеет вид
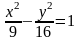 ,
то длина ее действительной полуоси
равна…
,
то длина ее действительной полуоси
равна…
16 2) 3 3) 9 4) 4
Уравнение прямой, перпендикулярной прямой у=2х+3, является…
1)2х-у+1=0 2) х+2у+4=0 3) 3х-у-5=0 4) х+3у+12=0
Укажите соответствие между кривыми второго порядка и их уравнениями:
А) парабола; Б) гипербола ; В) эллипс; Г) окружность.
Укажите соответствие между уравнением плоскости и ее положением в пространстве
А) плоскость хОz; Б) параллельна плоскости хОz;
В) параллельна плоскости уОz; Г) параллельна плоскости хОу;
Д) плоскость хОу.
Установите соответствие между уравнением плоскости и точками, которые лежат в этих плоскосях
А) (5; -1; 7); Б) (0; 0; 0); В) (1; 1; 1); Г) (1; 1; 0); Д) (-2; 0; 0)
Дана матрица
 тогда
сумма элементов, расположенных на
главной диагонали этой матрицы, равна…
тогда
сумма элементов, расположенных на
главной диагонали этой матрицы, равна…
1) 5 2) -5 3) -7 4) 13
Алгебраическое дополнение элемента а32 матрицы
 имеет
вид…
имеет
вид…
1)
 2)
2)
 3)
3)
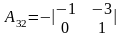 4)
4)

Дана система линейных уравнений
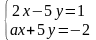 .
Система не имеет решений при а
равном…
.
Система не имеет решений при а
равном…
1)-0,5 2) 0 3) -2 4) 2