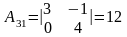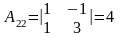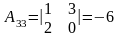- •Методические указания
- •Введение
- •Методические указания к расчетно-графическим работам
- •Варианты контрольных заданий. Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 23
- •Вариант 24
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Тестовые задания по темам: «Элементы линейной алгебры», «Элементы аналитической геометрии», «Элементы векторной алгебры».
- •Список рекомендованной литературы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Филиал федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
имени Т.Ф. Горбачева» в г. Прокопьевске
КАФЕДРА ЕСТЕСТВЕННОНАУЧНЫХ ДИСЦИПЛИН
Методические указания
для студентов технических специальностей очной формы обучения по темам:
«Элементы линейной алгебры», «Элементы аналитической геометрии»,
«Элементы векторной алгебры»
Составители: Л.И. Мамонова
С.В.Микова
И.Н. Чайковская
Утверждены на заседании кафедры ЕНД
Протокол№5 от 16.12.2011г.
Прокопьевск - 2011
СОДЕРЖАНИЕ
Введение…………………………………………………………………………...4
Методические указания к расчетно-графическим работам…………………….4
Варианты контрольных заданий………………………………………………..13
Тестовые задания по темам……………………………………………………..32
Список рекомендуемой литературы……………………………………………37
Приложение………………………………………………………………………38
Введение
В данной работе предлагаются методические указания к расчетно-графическим работам для студентов очного факультета специальностей: «Открытые горные работы», «Подземная разработка пластовых месторождений», «Горные машины и оборудования», «Технология машиностроения», «Автомобили и автомобильное хозяйство», «Информационные системы и технологии», «Промышленное и гражданское строительство» по темам: «Элементы линейной алгебры», «Элементы аналитической геометрии», «Элементы векторной алгебры». Приведены примеры решения типовых задач и тестовые задания.
Контрольные задания составлены в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования с учетом обобщения рабочих программ по математике для бакалавров технических специальностей Кузбасского государственного технического университета.
Методические указания к расчетно-графическим работам
Для выполнения задания №1 необходимо использовать знания линейной алгебры.
Пример 1. Решить систему уравнений методом Крамера и с помощью обратной матрицы:
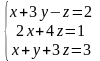
Решение. а)Решим систему по формулам Крамера. Для данной системы линейных уравнений определитель, составленный из коэффициентов при неизвестных, равен:
 Так
как определитель системы отличен от
нуля, то для ее решения можно воспользоваться
формулами Крамера:
Так
как определитель системы отличен от
нуля, то для ее решения можно воспользоваться
формулами Крамера:
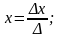


Получим решение системы:

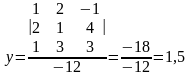
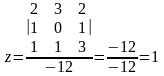
Ответ: (-1,5; 1.5; 1).
б)
Решим систему с помощью обратной матрицы.
Найдем матрицу А-1,
обратную к матрице системы

так
как
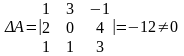 ,
то матрица А-1
существует
,
то матрица А-1
существует

Найдем алгебраические дополнения ко всем элементам матрицы А:

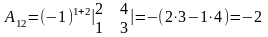

|
|
|
|
|
|
Значит

Найдем решение системы уравнений:
 ,
где
,
где


Ответ: х=-1,5; у=1,5; z=1 (как и при решении по формулам Крамера).
Пример 2. Решить систему уравнений методом Гаусса:

Решение. Для решения системы, у которой число уравнений не равно числу неизвестных, удобнее применить метод Гаусса. Приведем систему к треугольному виду. Можно записывать только матрицу коэффициентов:
 ~
~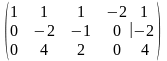 ~
~
rangA=rangА/B=2<n=3, где n – количество переменных системы, значит система совместна и имеет бесконечное множество решений.
Последняя матрица соответствует системе двух уравнений с четырьмя неизвестными:
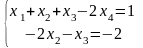
Примем за свободные неизвестные х3 и х4, перенесем их в правую часть уравнения и получим общее решение системы:
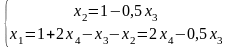
Придавая х3 и х4 различные значения, получим множество решений системы.
Ответ:
(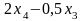 ;
; ;х3;
х4),
где х4
и
х3
–
любые.
;х3;
х4),
где х4
и
х3
–
любые.
Для выполнения задания №2 необходимо использовать знания аналитической геометрии на плоскости и в пространстве.
Пример 3. Даны координаты вершины пирамиды А1(1; 2; 3), А2(4; 6; 8), А3(-5; -7; -2), А4(-1; 9;0). Найти:
длину ребра А1А2;
угол между ребрами А1А2 и А1А4;
площадь грани А1А2А3;
объем пирамиды;
уравнение прямой А1А2;
уравнение плоскости А1А2А3. Сделать чертеж.
Решение.
В первом пункте нужно найти длину ребра А1А2. Ее следует определять как длину вектора.
Пусть
известны координаты точек А1(1;
2; 3) и А2(4;
6; 8). Найдем координаты вектора
 .
Тогда его длина
.
Тогда его длина
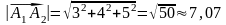 .
.
При определении угла между ребрами А1А2 и А1А4 нужно воспользоваться понятием скалярного произведения векторов и определить угол α между векторами
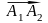 и
и
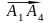 ,
имеющими общее начало.
,
имеющими общее начало.
Так
как даны вершины А1(1;
2; 3), А2(4;
6; 8) и А4(-1;
9;0), то определим координаты векторов
,
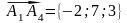 .
.
Найдем косинус угла α между векторами:
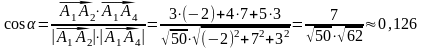
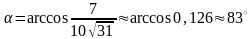 .
.
При определении площади грани А1А2А3 нужно использовать геометрический смысл векторного произведения.
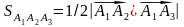
Так
как
,
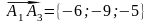 ,
то
,
то
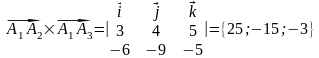 .
.
Тогда
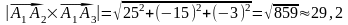

Для определения объема пирамиды следует изучить тему «Смешанное произведение векторов».
Возьмем векторы , , и составим смешанное произведение этих векторов.
Объем
пирамиды, построенной на этих векторах
равен:

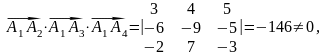

При решении данной задачи используют некоторые разделы аналитической геометрии. Так, при составлении уравнения прямой А1А2 используют канонические уравнения прямой в пространстве, проходящей через две данные точки.
Так
как А1(1;
2; 3), А2(4;
6; 8), то уравнение прямой А1А2
будет иметь вид
 или
или

Составляя уравнение плоскости А1А2А3, используем формулу уравнения плоскости, проходящей через данную точку М0(х0; у0; z0) перпендикулярно данному вектору
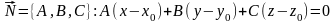
Причем за точку М0 можно взять любую из точек А1, А2, А3. Мы возьмем А1(1; 2; 3).
Так
как вектор N
перпендикулярен векторам
и
 ,
то
,
то
 ,
и для его определения необходимо изучить
тему «Векторное произведение».
,
и для его определения необходимо изучить
тему «Векторное произведение».
Так
как
,
,
то
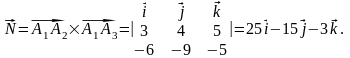
Уравнение плоскости А1А2А3 имеет вид 25(х-1)-15(у-2)-3(z-3)=0 или 25х-15у-3z+14=0.
При построении области решений системы неравенств в задании №3 необходимо знать уравнения прямых на плоскости и кривых второго порядка (приложение 1).
Пример
4.
Построить на плоскости область решений
системы неравенств:
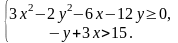
Решение. Построение областей следует начинать с построения ограничивающих их линий. Области решения данной системы неравенств ограничена линиями:
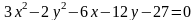 (кривая
второго порядка),
(кривая
второго порядка),
 (прямая
линия).
(прямая
линия).
Для построения кривой второго порядка ее необходимо привести к каноническому виду. Сгруппируем члены, содержащие только х и только у, и дополним их до полных квадратов:

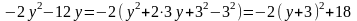
Уравнение
кривой имеет вид
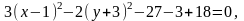
 .
.
Это
каноническое уравнение гиперболы с
центром в точке х0=1,
у0=
-3 и
полуосями а=2,
b= .
.
Посмотрим
эту кривую (см.прилож. 1) и найдем ту
область, которая удовлетворяет первому
неравенству. Эта часть плоскости, лежащая
между ветвями гиперболы, или внутри
ветвей. Возьмем произвольную точку
плоскости, например точку О(0;
0)
и подставим ее координаты в неравенство.
Получаем
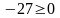 .
Неверно. Следовательно, точка О(0;
0)
и все точки той части плоскости, что
лежат между ветвями гиперболы, неравенству
не удовлетворяют. Заштрихуем область
решения первого неравенства вертикальными
линиями, это области внутри ветвей
гиперболы и сами ветви (рис. 1а).
.
Неверно. Следовательно, точка О(0;
0)
и все точки той части плоскости, что
лежат между ветвями гиперболы, неравенству
не удовлетворяют. Заштрихуем область
решения первого неравенства вертикальными
линиями, это области внутри ветвей
гиперболы и сами ветви (рис. 1а).
Переходим
ко второму неравенству. Граница области
прямая линия. Ее можно построить по двум
точкам х=2,
у= -9; х=6, у=3.
Чтобы определить область решения
неравенства
 ,
возьмем произвольную точку, например,
М(8;
0)
и подставим ее координаты в неравенство.
Получим 24>15. Верно. Следовательно,
точка М(8;
0)
и все точки, лежащие по ту же сторону от
прямой, удовлетворяют неравенству.
Заштрихуем эту область горизонтальными
линиями (рис. 1б).
Так как точки, лежащие на прямой
не удовлетворяют неравенству, проводим
прямую пунктирной линией.
,
возьмем произвольную точку, например,
М(8;
0)
и подставим ее координаты в неравенство.
Получим 24>15. Верно. Следовательно,
точка М(8;
0)
и все точки, лежащие по ту же сторону от
прямой, удовлетворяют неравенству.
Заштрихуем эту область горизонтальными
линиями (рис. 1б).
Так как точки, лежащие на прямой
не удовлетворяют неравенству, проводим
прямую пунктирной линией.
-
А)

Б)
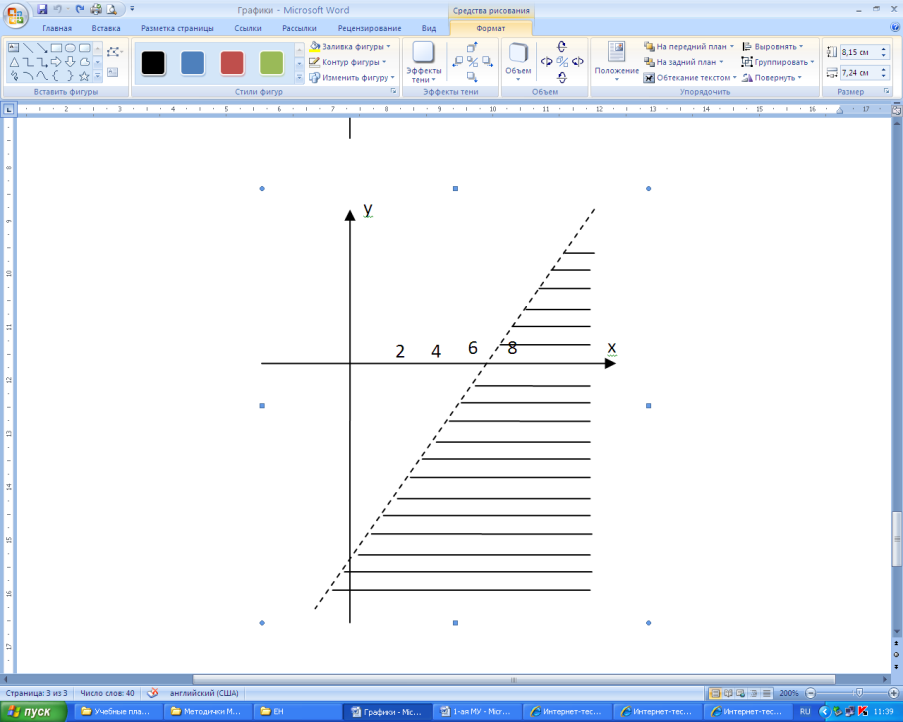
В)

Решение системы является общая часть (пересечение) областей решений каждого неравенства, т.е. область с двойной штриховкой (рис. 1в).