Фильтрация ких фильтров. Ких с конечной импульсной характеристикой Реализация цифровых фильтров

Физически реализуемый цифровой фильтр для формирования выходного сигнала в -ый момент времени может использовать следующие исходные данные:

• 

• 

Целые числа и определяют порядок цифрового фильтра. По этим значениям цифровые фильтры делятся на 2 основных вида: КИХ и БИХ

КИХ (нерекурсивный) фильтр соответствует случаю, когда и он работает в соответствии с алгоритмом

(3.13)

Для того, чтобы понять смысл входящих в данное выражение коэффициентов вернемся к выражению 3.10:

Сравнивая 3.10 и 3.13 можно сделать выводы:

1. Число отсчетов импульсной характеристики нерекурсивного цифрового фильтра ограничено значением . Если оно ограничено, значит это КИХ фильтр

2. Коэффициенты есть не сто иное, как значение отсчетов импульсной характеристики

Применим к обеим частям выражения 3.13 -преобразование. Получим:

Из этого выражения системная функция фильтра определяется как

(3.14)

Зарисуем структурную схему нерекурсивного цифрового фильтра:

Вследствие отсутствия обратной связи, цифровой фильтр КИХ структуры является абсолютно устойчивым. Устойчивость, простота анализа и реализации а так же наглядная связь коэффициентов фильтра с отсчетами его импульсной характеристики привели к тому, что данный тип фильтров широко применяется на практике

У него есть и недостатки: для получения хорошей частотной характеристики требуется нерекурсивный фильтр очень высокого порядка, т.е. число должно иметь размерность до нескольких сотен и даже тысяч

Рекурсивный (БИХ) фильтр соответствует случаю, когда и работает в соответствии с алгоритмом

(3.15)

Выполним -преобразование в обеих частях этого выражения:

Можно сказать, что импульсная характеристика рекурсивного цифрового фильтра имеет бесконечное число отсчетов, следовательно, это фильтр БИХ типа

Рекурсивный фильтр при меньшей сложности обеспечивает лучшие частотные характеристики, однако при наличии обратной связи в нем существует опасность потери устойчивости

Структурная схема БИХ-фильтра:

Таблица 5.1. Численные значения для примера усреднения

Индекс минуты	Количество машин за последнюю минуту	Среднее за последние 5 минут количество машин в минуту
1	10	-
2	22	-
3	24	-
4	42	-
5	37	27
6	77	40,4
7	89	53,8
8	22	53,4
9	63	57,6
10	9	52

Для вычисления текущего отсчета выходного сигнала КИХ фильтры используют только текущий и предыдущий отсчеты входного сигнала и совсем не используют выходные отсчеты. Если входная последовательность содержит конечное количество ненулевых отсчетов, то выходная последовательность такого фильтра так же будет содержать последовательность ненулевых отсчетов конечной длительности

Если входная последовательность, начиная с некоторого момента превращается в последовательность нулевых отсчетов, то через некоторое время выходная последовательность так же будет содержать только нулевые отсчеты

Для вычисления выходных отсчетов КИХ фильтры используют сложение примерно так же, как используется сложение в процессе усреднения. Таким образом, усреднение представляет собой КИХ фильтр

Рассмотрим пример: допустим, мы считаем количество машин, проходящих по мосту за минуту. Необходимо узнать среднее количество машин в минуту за интервал в 5 минут

Выходная последовательность оказывается намного более гладкой, чем входная. Это устройство усреднения ведет себя как ФНЧ, сглаживая быстрые изменения входной последовательности

Данное устройство является КИХ фильтром, т.к. он не использует предыдущие выходные отсчеты для вычисления текущего значения. Кроме того, если мост закрывается в конце 19-ой минуты, то первая линия быстро опускается до 0 машин в минуту в конце 20-й минуты. Выходные отсчеты устройства усреднения уменьшается до 0 в конце 24-й минуты

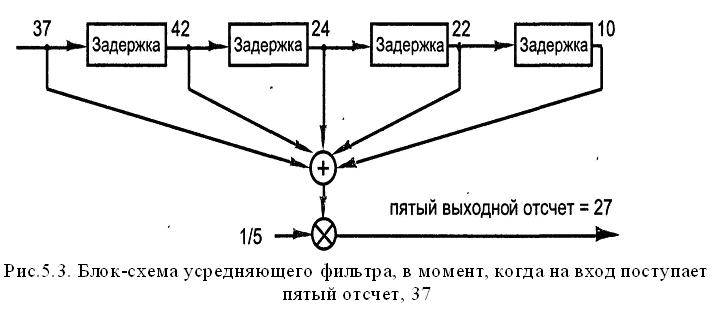
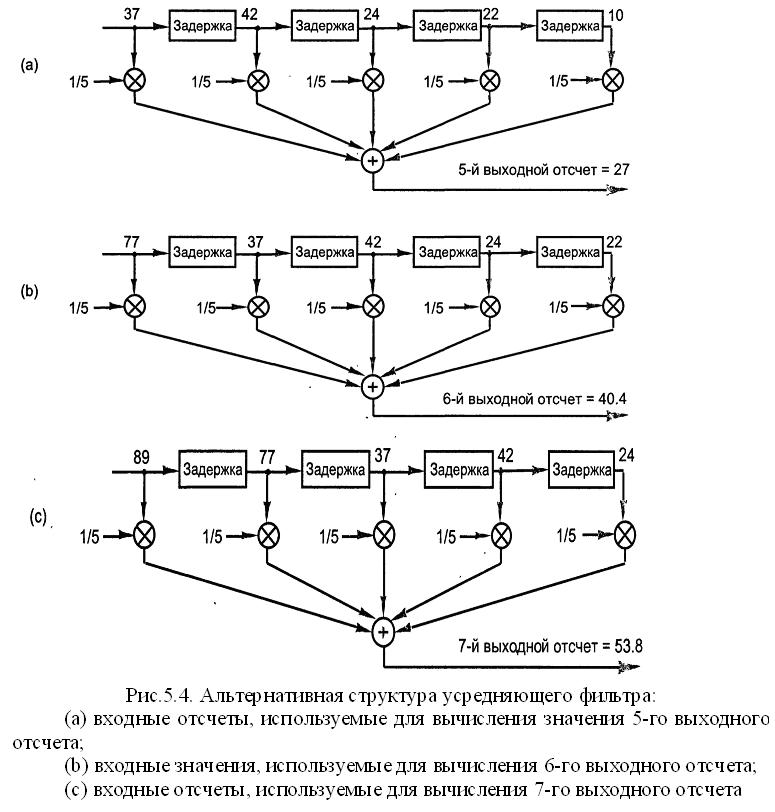
На рисунке обозначены элементы задержки. Они называются единичными задержками. Данную задачу можно было решать другим путем: можно было бы умножить каждое значением на , затем вычислить их сумму (5.4 А)

Наиболее интересный аспект понимания сущности КИХ фильтров связан с предсказанием их поведения при подаче на вход синусоидальных последовательностей разных частот, т.е. оценка их частотной характеристики. НА частотную характеристику КИХ фильтра влияют два фактора:

1. Количество ответвлений

2. Значения коэффициентов, используемые при умножении

В связи с тем, что первое значение уходит в небытие, КИХ фильтры называют так же трансверсальными, т.е. секущими. В данном случае это КИХ фильтр с 5 ответвлениями. Эти фильтры всегда устойчивы и проектируются на основе заданной импульсной характеристики