- •Цифровая обработка сигналов в радиоэлектронном оборудовании
- •Лекция 1. Основы анализа сигналов Классификация сигналов
- •Ряд Фурье
- •Связь между аналоговыми, дискретными и цифровыми сигналами
- •Спектральное представление сигналов Непериодические сигналы
- •Периодические сигналы и их спектр
- •Корреляционный анализ сигналов
- •Аналоговые системы
- •Классификация систем
- •Характеристики линейной стационарной системы
- •Дискретизация периодических сигналов. Дискретное преобразование Фурье (дпф)
- •Дискретная свертка сигналов. Z-преобразование дискретных сигналов
- •Корреляционный анализ дискретных сигналов
- •Представление дискретных сигналов и систем во временной и частотной области Импульсная характеристика дискретных систем
- •Цифровая фильтрация Цифровая фильтрация сигналов
- •Основные определения и классификация цифровых фильтров
- •Реализация цифровых фильтров. Нерекурсивный и рекурсивный фильтры
- •Фильтрация ких фильтров. Ких с конечной импульсной характеристикой Реализация цифровых фильтров
- •Аналоговый и цифровой трансверсальные фильтры
- •Бих фильтры Фильтры с импульсной характеристикой бесконечной длины
- •Бих фильтры первого и второго порядка
- •Двоичные числа Принцип построения чисел в позиционных системах счисления
Дискретизация периодических сигналов. Дискретное преобразование Фурье (дпф)
С периодическим сигналом
поступают следующим образом: в начале
его спектр ограничивают с помощью
фильтра с частотой среза, равной
эффективной ширине спектра сигнала
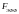 ,
затем на отрезке
,
затем на отрезке
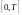 ,
где
- это период сигнала берут
,
где
- это период сигнала берут
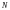 с интервалом
,
удовлетворяющим теореме Котельникова.
К полученным отсчетам применяют операцию,
которая называется ДПФ
с интервалом
,
удовлетворяющим теореме Котельникова.
К полученным отсчетам применяют операцию,
которая называется ДПФ
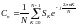
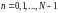
Полученные значений представляют собой комплексные амплитуды гармоник спектра сигнала . По ним можно восстановить исходный аналоговый сигнал по формуле:
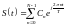
В частности, можно вернуться к отсчетам по формуле:
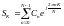
Выражения и являются дискретным аналогом обычной пары преобразований Фурье для непрерывных периодических сигналов. В настоящее время дискретный спектральный анализ является одним из главных методов исследования сигналов с помощью ЭВМ
Дискретная свертка сигналов. Z-преобразование дискретных сигналов
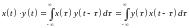 - свертка для аналоговых сигналов
- свертка для аналоговых сигналов
По аналогии со сверткой непрерывных
сигналов в теории дискретных систем
вводят дискретную свертку – сигнал,
отсчеты которого связаны с отсчетами
дискретных сигналов
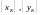 соотношением:
соотношением:
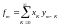
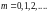
Пример: вычислить свертку дискретных сигналов:
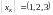
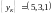
Решение:
Воспользовавшись алгоритмом дискретной
свертки, осуществим непосредственное
вычисление ее отсчетов. Для этого вначале
выпишем отсчеты сигнала
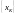 в прямой последовательности, а
в прямой последовательности, а
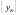 в обратной последовательности
в обратной последовательности
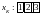
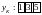
Чтобы определить нулевой отсчет свертки,
т.е.
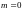 ,
совместим нулевые позиции полученных
сигналов:
,
совместим нулевые позиции полученных
сигналов:
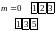
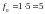
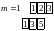
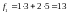
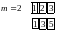
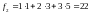
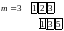
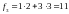
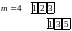
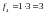
Итак,
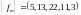
При математическом описании дискретных
сигналов и устройств, широко применяют
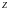 -преобразование,
которое является аналогом преобразования
Лапласа для непрерывных сигналов
-преобразование,
которое является аналогом преобразования
Лапласа для непрерывных сигналов
Пусть
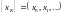 - это отсчетные значения некоторого
дискретного сигнала. Тогда прямое
-преобразование
определяется суммой ряда:
- это отсчетные значения некоторого
дискретного сигнала. Тогда прямое
-преобразование
определяется суммой ряда:
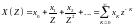 ,
где
- комплексная переменная
,
где
- комплексная переменная
Функция
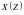 определена только для области комплексной
плоскости, в которой данный ряд сходится
определена только для области комплексной
плоскости, в которой данный ряд сходится
Основные свойства -преобразования:
-преобразование линейно, т.е. сумме двух дискретных сигналов соответствует сумма их -преобразований
Если
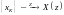 ,
то
,
то
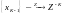 .
.
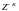 является оператором задержки на одну
позицию
является оператором задержки на одну
позициюЕсли
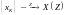 и
и
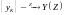 ,
то
,
то
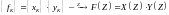 ,
т.е. свертке двух сигналов во временной
области соответствует произведение
-образов
этих сигналов
,
т.е. свертке двух сигналов во временной
области соответствует произведение
-образов
этих сигналов
Пример 2: найти -образы сигналов из предыдущего примера, т.е.
Решение:
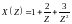
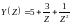
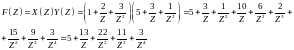
Сравнивая
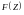 с результатом, полученным для
с результатом, полученным для
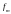 наблюдаем, что они идентичны
наблюдаем, что они идентичны
Корреляционный анализ дискретных сигналов
Для дискретных сигналов так же, как и
для аналоговых, вводится понятие АКФ с
той лишь разницей, что вместо операции
интегрирования используют суммирование,
а вместо переменной
 используют целое число
используют целое число
 ,
указывающее, на сколько позиций сдвинута
копия относительно исходного сигнала
,
указывающее, на сколько позиций сдвинута
копия относительно исходного сигнала
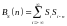 ,
где
,
где
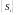 - отсчетное значение дискретного сигнала
- отсчетное значение дискретного сигнала
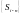 - отсчетное значение копии сигнала,
задержанное на
позиций
- отсчетное значение копии сигнала,
задержанное на
позиций
Эта функция обладает теми же свойствами, что и обычная АКФ, т.е.
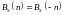
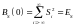 - энергия сигнала
- энергия сигнала
Вводится понятие ВКФ для дискретных сигналов:
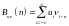
В случае цифровых сигналов, вычисление по формулам АКФ и ВКФ вычисляется с помощью ЦПОС.
Вопрос о корреляционных свойствах дискретного сигнала в радиоэлектронных устройствах часто возникает на уровне линии передачи сигналов. При этом текущее время разбивается на элементарные промежутки, называемые позициями. Эти позиции отсчитываются синхронно как на передающей, так и на приемной стороне линии связи. Синхронизация осуществляется путем периодической передачи специальных сигналов синхронизации.
На каждой позиции сигнал может принимать одно из трех значений: 0, +1, -1.
Если положение 0 – это означает отсутствие информации
Если +1 – это значит в данный момент передается логическая единица
Если -1 – в данный момент передается логический ноль
Обычно передача сообщений по линиям выглядит так:
При отсутствии сообщения в линии
наблюдаются одни нули, затем появляется
первый сигнал, который занимает
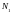 позиций и представляет собой некоторую
+1 и -1. Далее идет пауза, состоящая из
одних нулей, затем появляется второй
сигнал, занимающий
позиций и представляет собой некоторую
+1 и -1. Далее идет пауза, состоящая из
одних нулей, затем появляется второй
сигнал, занимающий
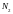 позиций и так далее
позиций и так далее
Пример трехпозиционного сигнала:
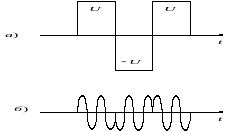
В случае А символу +1 соответствует положительное напряжение, символу -1 – отрицательное
В случае Б символу +1 соответствует отрезок колебания с нулевой начальной фазой, символу -1 соответствует отрезок колебания с начальной фазой . Такое фазовое кодирование подходит для беспроводных линий связи, где в качестве носителя используется высокочастотное колебание, называемое несущим
Оба случая могут быть записаны следующим образом:
…0001-11000…
АКФ данного сигнала: