Спектральное представление сигналов Непериодические сигналы
Любой непериодический сигнал может быть представлен в следующем виде:
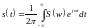- обратное преобразование Фурье
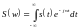- прямое преобразование Фурье
Этим записям есть альтернатива:
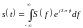
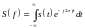
Эти уравнения являются спектральной плотностью сигналов
Это комплексные величины
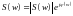
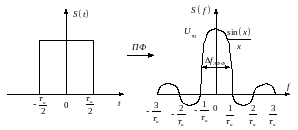
Сигнал конечной длительности имеет бесконечный спектр и наоборот: сигнал с конечным спектром имеет бесконечную длительность.
Для сигналов с бесконечной длительностью
вводится понятие эффективной ширины
спектра
,
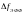под которой понимают ту область спектра,
которая несет заранее оговоренную долю
энергии всего сигнала
Для нахождения используется формула энергии сигнала:
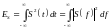
Энергия любого сигнала есть результат
суммирования вкладов от различных
интервалов частотной оси. Таким образом,
если исходить из 90%-го критерия, эффективная
ширина спектра прямоугольного
видеоимпульса будет равна
.
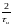Это касается двустороннего представления
спектра, где фигурируют и положительные,
и отрицательные частоты
90% энергии прямоугольного импульса
несут частоты от 0 до
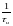
Для сигналов конечной длительности база сигнала обозначается в виде буквы:
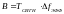
Периодические сигналы и их спектр
Любой сложный периодический сигнал может быть представлен в виде:
,
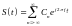где
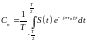
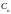- комплексная амплитуда
-ой
гармоники
Данная формула – преобразование Фурье для периодических функций (ряд Фурье)
Запишем спектр периодической
последовательности прямоугольных
импульсов. В отличии от одиночного
импульса, спектр периодической
последовательности импульсов имеет
дискретную структуру с шагом
:
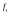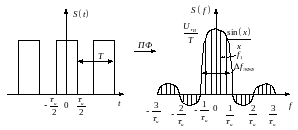
Для периодических сигналов так же
вводится понятие эффективной ширины
спектра, под которой понимают ту область
частот, которая несет заранее оговорённую
долю средней мощности сигнала. Для
нахождения
используют формулу для нахождения
средней мощности сигнала
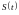
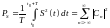
Корреляционный анализ сигналов
Смысл корреляционного анализа состоит
в количественном измерении степени
сходства различных сигналов. Для
непериодического сигнала
с конечной энергией
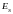вводится понятие автокорреляционной
функции (АКФ)
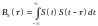
АКФ количественно оценивает степень
отличия сигнала
и его смещенной по времени копии
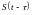
Свойства АКФ:
1.
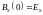
2.
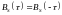
3.
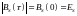
4.
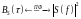- квадрат модуля спектральной плотности
т.к.
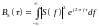и
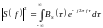
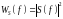- спектральная плотность энергии
Для периодического сигнала
,
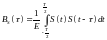где
- некоторый интервал наблюдения
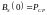- средняя мощность сигнала
Для большинства практических сигналов,
АКФ затухает с ростом времени
.
Для количественной оценки затухания
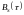вводится понятие радиуса корреляции
.
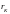Это значение времени
,
при котором значение
затухает до пренебрежимо малых значений
В радиоэлектронике особый интерес проявляют к сигналам с узкой АКФ (малым радиусом корреляции ). Таким свойством обладают сигналы с широкой базой. Чтобы понять разницу между корреляционным и спектральным анализом сигналов, необходимо сопоставить формулы корреляционного и спектрального анализа:
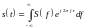- спектральная плотность сигнала
Исходя из этих формул, АКФ нечувствительно к фазовым соотношениям спектра сигнала, тогда как форма сигнала во времени к ним очень чувствительна. Другими словами, АКФ является более грубым инструментом анализа структуры сигналов, но зато и более устойчивым к изменчивости формы сигнала, возникающей из-за фазовых искажений
Если применить формулу
к двум разным сигналам, то получим ВКФ – взаимную корреляционную функцию
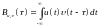
Чаще всего интересуются значением
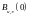
Структурная схема коррелятора:
…
…
…
…
…
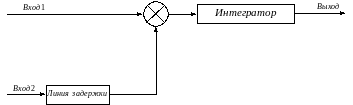
Схема обработки аналоговых и цифровых сигналов:
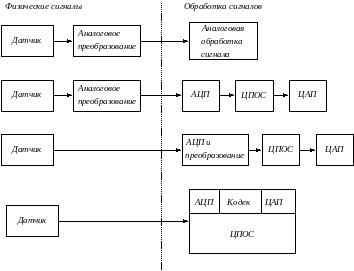
Как только выбрана технология цифровой обработки, должно быть определено месторасположение АЦП в тракте обработки сигнала. АЦП расположено ближе к датчику, поэтому большая часть обработки аналогового сигнала производится посредством АЦП. Увеличение возможностей АЦП может выражаться:
В увеличении частоты дискретизации
В расширении динамического диапазона
Повышение разрешающей способности
Отсечение входного шума
Использование входной фильтрации и программируемых усилителей
В наличие источников опорного напряжения на кристалле и т.д.
Все упомянутые дополнения повышают функциональный уровень и упрощают схему
Обработка сигналов в реальном времени, цифровая обработка сигналов:
ширина спектра обрабатываемого сигнала ограничена частотой дискретизации АЦП, ЦАП.
динамический диапазон сигнала ограничен разрядностью АЦП, ЦАП
производительность процессора обработки сигнала ограничивает объем обработки сигнала, т.к. для работы в реальном масштабе времени вес вычисления, производимые ЦПОС, должны быть закончены в течение интервала дискретизации, равного
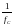
Нельзя забывать об аналоговой обработке сигнала при высокочастотной радиочастотной фильтрации, модуляции, демодуляции, там, где диктуется здравый смысл и экономические выкладки