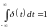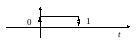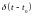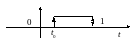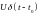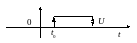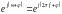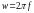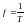- •Цифровая обработка сигналов в радиоэлектронном оборудовании
- •Лекция 1. Основы анализа сигналов Классификация сигналов
- •Ряд Фурье
- •Связь между аналоговыми, дискретными и цифровыми сигналами
- •Спектральное представление сигналов Непериодические сигналы
- •Периодические сигналы и их спектр
- •Корреляционный анализ сигналов
- •Аналоговые системы
- •Классификация систем
- •Характеристики линейной стационарной системы
- •Дискретизация периодических сигналов. Дискретное преобразование Фурье (дпф)
- •Дискретная свертка сигналов. Z-преобразование дискретных сигналов
- •Корреляционный анализ дискретных сигналов
- •Представление дискретных сигналов и систем во временной и частотной области Импульсная характеристика дискретных систем
- •Цифровая фильтрация Цифровая фильтрация сигналов
- •Основные определения и классификация цифровых фильтров
- •Реализация цифровых фильтров. Нерекурсивный и рекурсивный фильтры
- •Фильтрация ких фильтров. Ких с конечной импульсной характеристикой Реализация цифровых фильтров
- •Аналоговый и цифровой трансверсальные фильтры
- •Бих фильтры Фильтры с импульсной характеристикой бесконечной длины
- •Бих фильтры первого и второго порядка
- •Двоичные числа Принцип построения чисел в позиционных системах счисления
Цифровая обработка сигналов в радиоэлектронном оборудовании
Преподаватель: Павлушкин Эрик Жоржевич
Лекция 1. Основы анализа сигналов Классификация сигналов
Сигнал – это функциональная зависимость одной величины от другой
Чаще всего рассматривается зависимость от времени следующих величин: напряжения, токов, напряженности ЭМП и других
Под сигналом понимают обнаруживаемую некоторую физическую величину или импульс, изменение которого во времени и пространстве несет нам полезную информацию об интересующем объекте или явлении
Сигналы классифицируются по определенным критериям:
Детерминированные, где значение
|
|
Случайный. Определить точное значение с точностью невозможно |
|
Непрерывные |
|
Импульсные |
|
Периодические |
|
Непириодические
|
|
Конечной длительности |
|
Бесконечной длительности |
|
Аналоговые. Они существуют в любой
момент времени
|
|
Дискретные. Данные сигналы существуют только в определенные моменты |
|
Цифровые |
|
Сигналы с интегрированным квадратом.
Для таких сигналов выполняется
следующие соотношение:
|
|
Сигналы с интегрированным квадратом. Для таких сигналов выполняется следующие соотношение:
Периодичность:
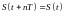 при любых
при любых
Среди множества сигналов есть несколько, играющих важную роль в радиоэлектронике
Функция включения (Хэвисайда)
|
|
Смещенная функция Хэвисайда
|
|
Функция Хэвисайда с амплитудой
|
|
|
|
Смещенная функция Дирака
|
|
Функция Дирака с амплитудой
|
|
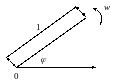
Комплексная периодическая функция
|
|
Сигналы оконечной длительности (финишные сигналы)
Очень важную роль в технике обработки сигналов играют гармонические колебания:
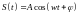
Этот сигнал является тестовым сигналом, который применяется для анализа характеристик цепей. Так же к тестовым сигналом относятся функция Дирака и функция Хэвисайда
Важное свойство функции – это фильтрующее свойство. Это значит, что функция присутствует под интегралом в качестве множителя. В этом случае результат интегрирования будет равен значению остального подынтегрального выражения в той точке, где сосредоточен импульс
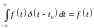
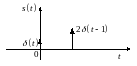
Функцию Хэвисайда удобно использовать
для создания математических выражений
для сигналов конечной длительности.
Она используется для формирования
прямоугольного импульса с амплитудой
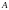 и длительностью
и длительностью
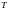

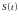 известно в любой момент времени
известно в любой момент времени
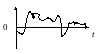
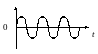

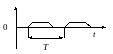

 и могут принимать любые значения в
интервале
и могут принимать любые значения в
интервале
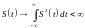
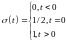

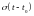
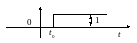
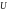
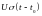
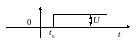
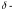 функция
Дирака
функция
Дирака ,
причем
,
причем