7. Моделювання двигуна постійного струму послідовного збудження

Двигуни постійного струму послідовного збудження (серієсні двигуни) до цього часу широко використовуються в тягових електроприводах, зокрема, в електричному транспорті, завдяки своїм механічним характеристикам.

Обмотка збудження ввімкнена в якірне коло послідовно з обмоткою якоря, потужність якої значно більша (порядків на два), ніж послідовної. Це призводить до форсування збудження на початкових стадіях пуско-гальмівних режимів, у результаті чого магнітний потік змінюється в широкому діапазоні. Така швидка зміна магнітного потоку зумовлює появу вихрових струмів в полюсах і станині аналогічно, як і в двигунів незалежного збудження, якщо швидкість регулювати збудженням двигуна. Розмагнічувальну дію вихрових струмів будемо враховувати, складаючи модель двигуна, наявністю на головних полюсах фіктивної короткозамкненої обмотки (рис. 1 .19), яка має умовні витки w_k , опір R_k та струм i_k (див. модель генератора). Індуктивність якірного кола приймається незмінною, реакцію якоря не враховуємо, залежність  = k_ФF вважаємо лінійною в околі робочої точки кривої  = f(F). Такі допущення дають можливість вважати модель лінійною.

рис. 1.19. Двигун постійного струму послідовного збудження в перехідних режимах

Запишемо систему рівнянь електричної, магнітної та механічної рівноваг, які описують динамічні процеси в двигуні, таким чином:

Перше рівняння системи поділимо на , а останній його член домножимо на і, позначивши , , отримаємо в операторній формі

,

Друге рівняння поділимо на R_k , а праву його частину домножимо на і отримаємо

.

З третього рівняння системи (2.24) виключимо i_k і, об’єднавши з четвертим, визначимо s у такій послідовності:

;

.

За одержаними виразами побудуємо структурну модель, яка показана на рис. 1 .20.

рис. 1.20. Структурна модель ДПС послідовного збудження з врахуванням вихрових струмів

Для серієсних двигунів, як і для двигунів незалежного збудження з регулюванням потоку середньої та великої потужності (більшої за 50 кВт) можна прийняти T_k  (0,1…0,2)T_d , і чим більша потужність, тим більше значення T_k .

Математичну модель, до складу якої входять диференціальні рівняння першого порядку, що подані нормальною формою Коші, зручно записувати, користуючись структурною моделлю (рис. 1 .20), яка має у своєму складі три динамічні ланки – дві аперіодичні та одну інтегральну, таким чином:

Якщо знехтувати ефектом дії вихрових струмів, то модель суттєво спрощується. Виходимо з таких рівнянь:

Нескладні перетворення призводять до математичної і структурної (рис. 1 .21) моделей.

рис. 1.21. Структурна модель ДПС послідовного збудження без врахування вихрових струмів

До п. 4.1

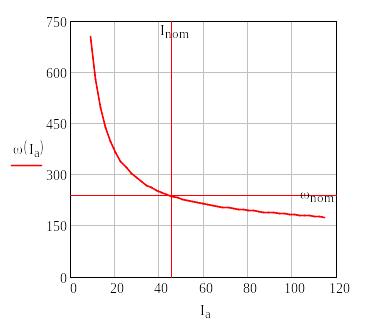
Нижче пропонується фрагмент варіанту розрахунку пускової характеристики ДПС послідовного збудження в середовищі MathCAD. Спосіб знаходження коефіцієнтів апроксимації розглянуто раніше для моделі генератора постійного струму.

MathCAD

… Далі аналогічно до ДПС незалежного збудження з врахуванням зміни сталої двигуна С у залежності від якірного струму … … Далі аналогічно до ДПС незалежного збудження