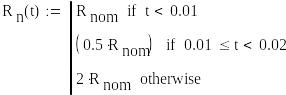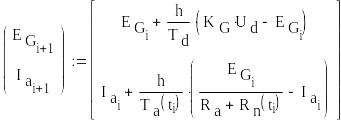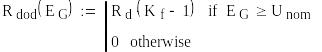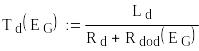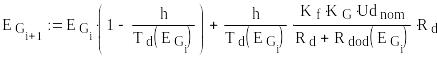3. Моделювання елементів електроприводів різницевими рівняннями

Аперіодична ланка описується диференціальним рівнянням першого порядку

або ,

де T – стала часу ланки;

k – коефіцієнт підсилення ланки;

x – вхідний сигнал.

З використанням для інтегрування явної формули Ейлера першого порядку

підставляючи значення похідної у формулу числового методу отримаємо

,

звідки .

Аналогічно, з використанням для інтегрування неявної формули Адамса другого порядку, яка є однією з найкращих формул для цієї мети завдяки своїй простоті та числовій стійкості,

отримаємо

,

звідки після спрощень матимемо

.

Потрібно відзначити, що використання неявних числових методів не тільки не ускладнює задачу, а й призводить до отримання рекурентних рівнянь з вищими стійкістю та точністю порівняно з використанням явних методів.

До п. 1.2.

Приклад розв'язування задачі з використанням методу Ейлера для дослідження режимів зміни навантаження генератора постійного струму подано нижче для середовища MathCAD.

MathCAD

Unom : = 230 Номінальна напруга на якорі генератора Ud : = 220 Номінальна напруга збудження генератора KG : = 1.045 Коефіцієнт підсилення генератора Td : = 0.8 Стала часу збудження генератора Ra : = 0.27 Опір якоря генератора La : = 0.0035 Індуктивність якоря генератора Rnom : = 5.1 Опір номінального навантаження La : = 0.0035 Індуктивність якоря генератора h : = 0.001 Крок моделювання Tmax : = 0.06 Тривалість перехідного процесу Кількість точок перехідного процесу i : = 0 .. 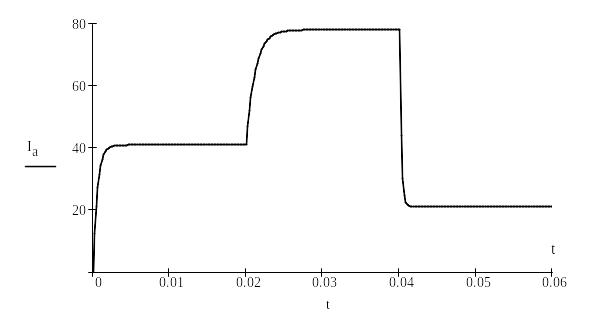N ti : = ih Значення часу Початкові умови: Залежність опору навантаження від часу: Залежність електромагнітної сталої часу якірного кола від опору навантаження: Знаходження значень напруги і струму якоря за формулою Ейлера Виведення графіка струму в навантаженні

4. Модель генератора постійного струму

Опис кола збудження є однаковим як для генератора постійного струму (ГПС), так і для двигуна постійного струму (ДПС), що працює зі змінним потоком.

Очевидним є те, що змоделювати, тобто, відтворити в моделі ті динамічні процеси, які відбуваються в оригіналі, наприклад, генераторі постійного струму, абсолютно точно неможливо. Мову можемо вести тільки про наближення, про отримання результатів моделювання з деякою точністю, яка значною мірою визначається допущеннями, які ми приймаємо, створюючи модель. Так, генератор постійного струму в неробочому режимі, коли якірне коло розімкнене, з достатньою для багатьох застосувань точністю можна розглядати як аперіодичну ланку першого порядку за таких допущень:

• не враховуємо нелінійність кривої намагнічування;

• нехтуємо вихровими струмами в станині (це цілком справедливо для генераторів зі шихтованою станиною);

• потоки розсіювання обмотки збудження генератора (ОЗГ) пропорційні струмові збудження.

а) електрична схема	б) структурна модель

рис. 1.6. Коло збудження ГПС

У випадку врахування навантаження (замкнуте якірне коло) приймаються додаткові допущення:

• індуктивність якоря незмінна;

• трансформаторною ЕРС у колі якоря нехтуємо;

• величина дії реакції якоря в залежності від точності моделі або не враховується, або приймається пропорційною струмові якоря.

Найпростіша математична модель ГПС базується на рівнянні електричної рівноваги кола збудження

та рівнянні ,

де U_d – напруга збудження генератора;

i_d – струм кола збудження генератора;

R_d – опір обмотки збудження генератора (ОЗГ);

L_d = L_ + L_s – індуктивність ОЗГ, яка має дві складові:

L_ – індуктивність намагнічування;

L_s – індуктивність розсіювання;

e_G – електрорушійна сила (ЕРС) якоря генератора;

K_G – коефіцієнт підсилення генератора за напругою.

Виконаємо нескладні перетворення диференціального рівняння, помноживши його на K_G , а останній член – на , після чого отримаємо

.

Позначивши – електромагнітна стала часу ОЗГ і , отримаємо

.

Це є спрощена математична модель генератора постійного струму, що описує перехідні процеси генератора без навантаження (режими неробочого ходу).

Для активного навантаження (рис. 1 .7) L_a + L_н = 0, тому струм якоря i_a обчислюється за виразом ,

де R_a = R_a + R_н – сумарний опір якірного кола;

R_a – опір якоря ГПС;

R_н – опір навантаження в якірному колі

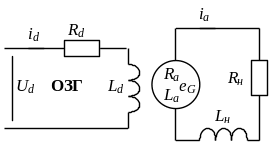
а) електрична схема	б) структурна модель

рис. 1.7. Генератор постійного струму

З урахуванням індуктивностей обмотки якоря L_a і навантаження L_н до диференціального рівняння опису кола ОЗГ додається ще одне: (див. рис. 1 .7). Поділивши це рівняння на R_a і позначивши – електромагнітна стала часу якірного кола, отримаємо диференціальне рівняння якірного кола, яке разом з рівнянням кола збудження є математичною моделлю ГПС:

Значення індуктивності намагнічування ОЗГ L_ та індуктивності обмотки якоря L_a машини постійного струму (якщо ці дані відсутні в каталозі) можна розрахувати за формулами:

і ,

де p_п – число пар полюсів;

W_p – число витків одного полюса ОЗГ;

 – магнітний потік одного полюса ОЗГ;

F – ампер-витки ОЗГ;

k – емпіричний коефіцієнт:

k = 0,6 для некомпенсованих машин;

k = 0,15 для компенсованих машин;

_н – номінальна частота обертання якоря генератора.

Значення індуктивності розсіювання обмотки збудження L_s машини постійного струму можна знайти за наближеною формулою , де  – коефіцієнт розсіювання, приблизно дорівнює 0,1 ... 0,2 (для потужніших машин – менше значення), а точніше обчислюється за формулою

,

де  – повітряний проміжок під полюсом у сантиметрах;

D – діаметр якоря у сантиметрах;

l – довжина якоря у сантиметрах.

Точнішу модель генератора, що враховує нелінійність кривої намагнічування, можна отримати за умови апроксимації характеристики намагнічування функцією арктангенса [²]:

У цьому випадку для отримання вищої точності в моделі генератора залежність e_G(i_d) апроксимується залежністю , де A, B – коефіцієнти апроксимації. Коефіцієнти апроксимації для першого наближення вибираються таким чином: A = E_Gн , тоді , звідки , після чого можливе їх уточнення ітераційним чи якимось іншим методом (для цього дуже зручно використовувати математичний пакет MathCAD). Така апроксимація є простою і, в той же час, забезпечує похибку не гірше (1-2)%, а за плавністю та точністю відтворення похідної має переваги перед іншими, наприклад, поліноміальними.

Реалізований в пакеті MathCAD приклад знаходження апроксимаційної залежності для напруги і ампер-витків обмотки збудження генератора подано нижче.

MathCAD

N : = 6 Кількість точок робочої характеристики i : = 0 .. N Побудова графіка апроксимаційної кривої та експериментальних точок

За відсутності даних про криву намагнічування у технічному паспорті генератора, можна скористатися універсальною кривою намагнічування [³] (рис. 1 .8), якій відповідають коефіцієнти апроксимації A = 0,858 і B = 2,351, тобто, вихідна напруга генератора буде апроксимуватися залежністю .

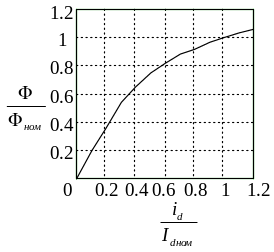
рис. 1.8. Універсальна крива намагнічування

Практичне застосування знайшла також й інтерполяція кривої намагнічування сплайнами [⁴, ⁵, ⁶], що також відповідає вимогам точності та гладкості, але потребує відповідного програмного забезпечення для реалізації цього підходу. Засоби апроксимації сплайнами реалізовані у математичних пакетах MathCAD і MATLAB і можуть доволі просто використовуватися [Error: Reference source not found, ⁷, ⁸, ⁹, ¹⁰]. Обидва способи наближення кривої намагнічування практично рівноцінні щодо точності та витрат комп’ютерного часу.

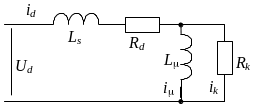
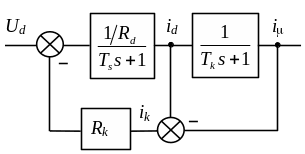
Підвищити точність відтворення реальних процесів у колі збудження генератора постійного струму з масивною станиною можна, якщо врахувати розмагнічувальну дію вихрових струмів у станині [¹¹, ¹²]. Для цього в електричну схему моделі кола збудження вводиться додатковий контур R_k – L_ , що імітує дію вихрових струмів (рис. 1 .9, а). Ввівши позначення T_k = L_ /R_k (стала часу контуру вихрових струмів), T_ = L_ /R_d , T_s = L_s /R_d можна побудувати структурну схему, показану на рис. 1 .9, б.

	або
а) електрична схема	б) структурна модель

рис. 1.9. Схема і структурна модель генератора постійного струму з врахуванням контуру вихрових струмів

Така модель описується системою диференціальних і алгебричних рівнянь:

або

де i_ – струм намагнічування;

i_k – струм контуру імітації вихрових струмів,

звідки можна отримати вирази в операторній формі для струмів збудження та намагнічування:

;

.

Для більшості генераторів постійного струму з масивною станиною стала часу еквівалентного контуру вихрових струмів T_k складає 15% ... 30% від сталої часу обмотки збудження T_G . Точніше значення сталої часу T_k знаходиться за емпіричною формулою [Error: Reference source not found]:

;

де l_j – довжина силової лінії у спинці між полюсами у сантиметрах;

a, b – товщина і довжина спинки станини у сантиметрах;

k_ = 210⁴ (для сталі).

Збільшення швидкодії систем з великими сталими часу, наприклад, обмоткою збудження, досягається шляхом використання форсованого режиму – перевищенням напруги збудження U_d номінальної величини в декілька разів. У цьому разі після досягнення номінального режиму e_G = U_ном напругу збудження потрібно повернути назад до номінального значення, щоб уникнути аварійних режимів. Приклад найпростішої реалізації з використанням реле напруги для генератора постійного струму показано на рис. 1 .3. Для такої схеми величина додаткового опору R_дод вибирається з умови забезпечення номінального струму збудження після виходу на номінальний режим і обчислюється просто, виходячи із залежностей

– для номінального режиму;

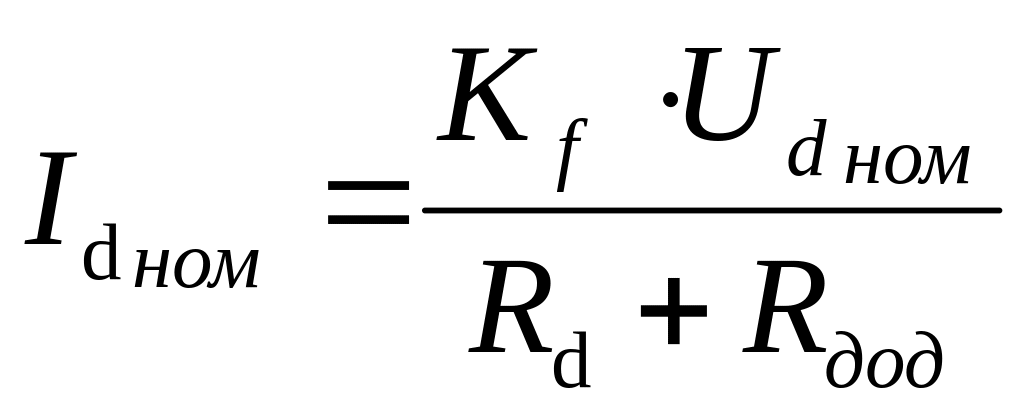– для режиму форсування;

звідси , де K_f – коефіцієнт форсування напруги збудження.

До п. 1.3.3.

Приклад розв'язування задачі з використанням методу Ейлера (див. стор. 15) для дослідження режиму форсованого пуску генератора постійного струму на неробочому ході (без врахування навантаження в колі якоря) подано нижче для середовища MathCAD.

MathCAD

Unom : = 230 Номінальна напруга на якорі генератора Ud : = 220 Номінальна напруга збудження генератора KG : = 1.045 Коефіцієнт підсилення генератора Ld : = 0.8 Індуктивність обмотки збудження генератора Rd : = 82 Опір обмотки збудження генератора Kf : = 2.5 Коефіцієнт форсування h : = 0.001 Крок моделювання Tmax : = 0.5 Тривалість перехідного процесу Кількість точок перехідного процесу i : = 0 .. 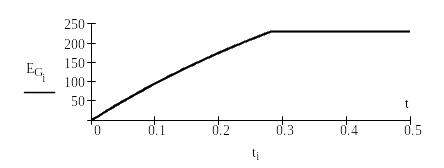N t0 : = 0 Значення часу ti+1 : = h(i + 1) Залежність додаткового опору від ЕРС генератора (імітація реле напруги): Залежність сталої часу обмотки збудження від додаткового опору: Знаходження ЕРС генератора під час форсованого пуску за формулою Ейлера: Виведення графіка ЕРС