
Изложение метода
Основная задача метода штрафных функций состоит в преобразовании задачи минимизации функции
![]()
с соответствующими ограничениями, наложенными на х, в задачу поиска минимума без ограничений функции
![]()
Функция
![]() является
штрафной. Необходимо, чтобы при нарушении
ограничений она «штрафовала» функцию
Z, т.е. увеличивала её значение.В этом
случае минимум функции Z будет находиться
внутри области ограничений. Функция
,
удовлетворяющая этому условию, может
быть не единственной. Задачу минимизации
можно сформулировать следующим образом:
является
штрафной. Необходимо, чтобы при нарушении
ограничений она «штрафовала» функцию
Z, т.е. увеличивала её значение.В этом
случае минимум функции Z будет находиться
внутри области ограничений. Функция
,
удовлетворяющая этому условию, может
быть не единственной. Задачу минимизации
можно сформулировать следующим образом:
минимизировать функцию
при
ограничениях
![]() .
.
Функцию удобно записать следующим образом:
![]()
где r – положительная величина.
Тогда
функция
![]() принимает
вид
принимает
вид
![]() .
.
Если
х принимает допустимые значения, т.е.
значения, для которых
![]() ,
то Z принимает значения, которые больше
соответствующих значений
,
то Z принимает значения, которые больше
соответствующих значений
![]() (истинной
целевой функции данной задачи), и разность
можно уменьшить за счет того, что r может
быть очень малой величиной. Но если х
принимает значения, которые хотя и
являются допустимыми, но близки к границе
области ограничений, и по крайней мере
одна из функций
(истинной
целевой функции данной задачи), и разность
можно уменьшить за счет того, что r может
быть очень малой величиной. Но если х
принимает значения, которые хотя и
являются допустимыми, но близки к границе
области ограничений, и по крайней мере
одна из функций
![]() близка
к нулю, тогда значения функции
,
и следовательно значения функции Z
станут очень велики. Таким образом,
влияние функции
состоит
в создании «гребня с крутыми краями»
вдоль каждой границы области ограничений.
Следовательно, если поиск начнется из
допустимой точки и осуществляется поиск
минимума функции
близка
к нулю, тогда значения функции
,
и следовательно значения функции Z
станут очень велики. Таким образом,
влияние функции
состоит
в создании «гребня с крутыми краями»
вдоль каждой границы области ограничений.
Следовательно, если поиск начнется из
допустимой точки и осуществляется поиск
минимума функции
![]() без
ограничений, то минимум, конечно, будет
достигаться внутри допустимой области
для задачи с ограничениями. Полагая r
достаточно малой величиной, для того
чтобы влияние
было
малым в точке минимума, мы можем сделать
точку минимума функции
без
ограничений совпадающей с точкой
минимума задачи с ограничениями.
без
ограничений, то минимум, конечно, будет
достигаться внутри допустимой области
для задачи с ограничениями. Полагая r
достаточно малой величиной, для того
чтобы влияние
было
малым в точке минимума, мы можем сделать
точку минимума функции
без
ограничений совпадающей с точкой
минимума задачи с ограничениями.
Алгоритм метода штрафных функций
Пусть
имеется следующая задача: Минимизировать
при
ограничениях
![]() ,
,![]() .
.
Начальный
этап
Выбрать
![]() в
качестве константы остановки, начальную
допустимую точку
в
качестве константы остановки, начальную
допустимую точку
![]() ∈
∈![]() ,
для которой
,
для которой
![]() ,
,
скаляр
,
,
скаляр
![]() и
и
![]() .
Положить k=1 и перейти к основному этапу.
.
Положить k=1 и перейти к основному этапу.
Основной этап. k-я итерация.
Первый
шаг.
При исходной точке
![]() решить
следующую задачу безусловной оптимизации:
решить
следующую задачу безусловной оптимизации:
![]() минимизировать,
где
минимизировать,
где
![]() -
параметр, значения которого убывают с
каждой итерации
-
параметр, значения которого убывают с
каждой итерации
![]() при
при
![]() ;
;
![]() -
положительные весовые коэффициенты.
-
положительные весовые коэффициенты.
Примерами штрафных функций являются:
1)
обратная функция
![]()
2)
логарифмическая функция
![]()
Положить
![]() равным
оптимальному решению задачи минимизации
и перейти ко второму шагу.
равным
оптимальному решению задачи минимизации
и перейти ко второму шагу.
Минимизация штрафной функцию может быть выполнена любым методом безусловной оптимизации, например, градиентным.
Второй шаг
Если
![]() ,
то остановиться. Решение является
искомым.
,
то остановиться. Решение является
искомым.
В
противном случае положить
![]() .
Изменить
.
Изменить
![]() и
перейти к первому шагу (k+1)-й итерации.
и
перейти к первому шагу (k+1)-й итерации.
11. Аналитические методы решения оптимезационных задач. Метод наискорейшего подъема (спуска).

12. Численные методы решения оптимезационных задач. Метод случайного поиска..




13. Численные методы решения оптимезационных задач. Метод спуска по координатам..


14. Численные методы решения оптимезационных задач. Метод сканирования.


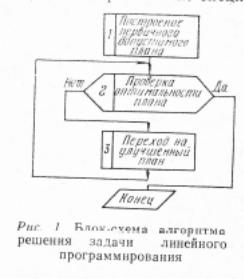
15. Метод линейного програмирования. Общие понятия. Общий алгоритм.

16. Транспортная задача линейного программирования. Общая постановка.




