Муниципальный этап 2008-2009 учебный год

10 Класс

1. Докажите, что число n²⁰⁰⁸ + 4 при любом натуральном n > 1 является составным.

2. Берем 2 дроби, из которых одна вдвое больше другой. Каждую дробь возводим в квадрат, результаты складываем, получаем некоторую сумму. Теперь каждую из первоначальных дробей возводим в куб, результаты складываем и замечаем, что опять получилась та же самая сумма. Найдите эту пару дробей.

3. Решите систему:

4. Имеется 2008 камней. Максим произвольно разбивает имеющиеся камни на 3 кучки, а затем они со Станиславом играют в следующую игру: каждым ходом разрешается взять любое число камешков из какой-либо одной кучки, либо любое одинаковое число камешков из любых двух кучек сразу. Проигрывает тот, кто возьмет последний камешек. Кто выигрывает при правильной игре, если первый ход делает Станислав?

5. В трапецию АВСД с основаниями АД = 10 и ВС = 2 можно вписать, а вокруг нее можно описать окружность. Определите, где (т. е. внутри, извне или на стороне) находится центр описанной около трапеции окружности.

ОТВЕТЫ, РЕШЕНИЯ, УКАЗАНИЯ.

10 Класс

1. n²⁰⁰⁸ + 4 = (n¹⁰⁰⁴ + 2)² – (2 n⁵⁰²)² = (n¹⁰⁰⁴ + 2 - 2 n⁵⁰²)·( n¹⁰⁰⁴ + 2 + 2 n⁵⁰²)

Второй множитель больше 1. В первом множителе произведем замену t = n⁵⁰², получим

t² -2 t + 2, что, очевидно, больше 1 при t > 1

(min (t² – 2t + 2) = 1 при t = 1).

2. Пусть искомые дроби: и (n, m Z, m ≠ 0).

Тогда , откуда 5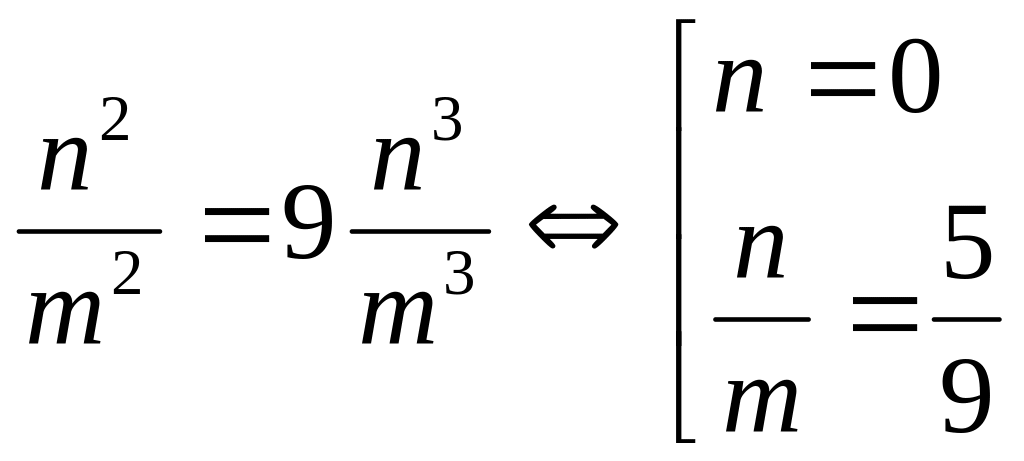

Случай n = 0 исключаем - получается не дробь.

Ответ: и .

3. Исходная система равносильна

следующей

Ответ: (1; 1; ... ; 1) или (-1; -1; ... -1).

4. Максим разбивает кучку камней на три следующим образом: 669, 669, 670. Далее, если Станислав берет n камней из одной кучки, то Максим берет по n камней из двух других, и наоборот.

Таким образом, кучки камней всегда будут иметь вид: (k, k, k+1), причем k с каждым ходом будет уменьшаться. В итоге получится (0, 0, 1), то есть Станислав возьмет последний камень и проиграет.

5. Из того, что трапеция вписанная следует, что она равнобедренная. Пусть х – боковая сторона. Из того, что в трапецию можно вписать окружность следует, что

х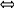 + х = 10 + 2 х = 6.

ВД² = 6² + 10² – 2 · 6 · 10 cos = 2² + 6² + 2 · 2 · 6 cos , откуда cos = .

Тогда ВД² = 56.

1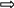 0² = 6² + 56 – 2 · 6 · cos cos < 0 АВД – тупой,

следовательно центр описанной около треугольника АВД окружности (а следовательно и около трапеции) лежит вне треугольника АВД – по другую от точки В (и точки С) сторону прямой АД.

Ответ: вне

2010 - 2011 Учебный год муниципальный этап

10 Класс

1. х + у + z = 1. Докажите, что х² + у² + z² ≥

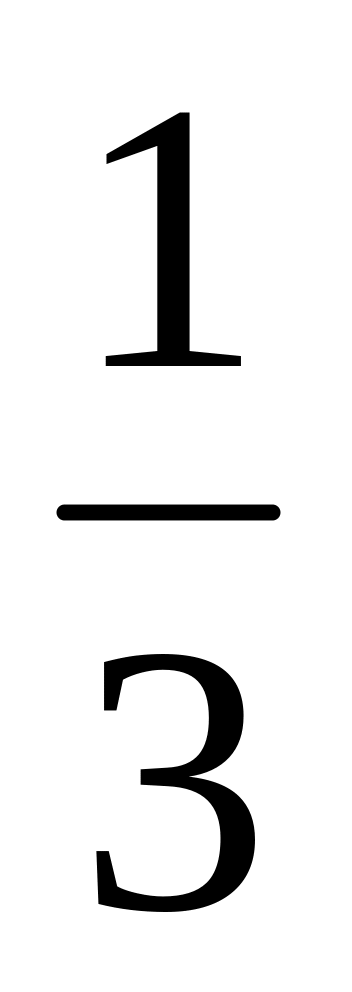
2. При каких а неравенство sin⁴x + cos⁴x > а sinxcosx выполнено при всех x?

3. Вне четырехугольника построены 4 вневписанных окружности с центрами О₁, О₂, О₃, О₄. Докажите, что около четырехугольника О₁О₂О₃О₄ можно описать окружность. (Окружность называется вневписанной, если она касается одной стороны и продолжения двух соседних с ней сторон.)

4. Из цифр 1, 2, 3, 4, 5, 6, 7 составляют всевозможные семизначные числа, в записи которых каждая цифра участвует только один раз. Докажите, что сумма всех этих чисел делится на 9.

5. В каждую клетку квадратной таблицы размера n х n (n – нечетное) вписана либо 1, либо -1 произвольным образом. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Может ли сумма всех 2n таких произведений быть равна 0?