Олимпиада 2012 - 2013г. Муниципальный этап Математика
10 Класс
Имеется квадратная таблица чисел (матрица):
,
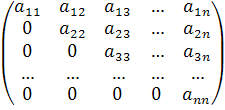где
числа
(то есть числа на диагонали) не равны
нулю. Все числа под диагональю равны
нулю. Возьмем из каждой строки и каждого
столбца по одному числу так, чтобы все
n
взятых чисел лежали в разных строках и
разных столбцах. После этого перемножим
взятые числа. Такое произведение назовем
цепочкой. Сколько среди всех возможных
цепочек таких, которые не равны нулю?
Пусть числа
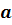и
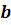таковы, что
.
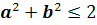Докажите, что
.
Длины катетов прямоугольного треугольника равны 2012 и 2. На его гипотенузе как на стороне во внешнюю сторону треугольника построен квадрат. Найдите расстояние от вершины прямого угла треугольника до центра квадрата.
В уравнении
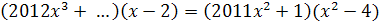одно из чисел стерто и заменено точками.
Известно, что число (-1) является корнем
этого уравнения. Решите это уравнение.Даны две перпендикулярные прямые. Найдите геометрическое место точек, сумма расстояний от которых до этих прямых равна 1.
10 Класс (решения)
Задание №1.
Решение: Покажем, что ненулевой является только цепочка , а все остальные цепочки будут иметь множитель из тех нулей, которые расположены под диагональю.
От противного. Пусть
существует другая цепочка, не содержащая
ноль. Тогда из первого столбца в этой
цепочке может быть только
.
Из второго столбца число
взять нельзя (так как уже взято число
из первой строки), поэтому из второго
столбца берется только
.
Рассуждая аналогично, получаем цепочку
,
что противоречит предложению о другой
возможной цепочке.
Ответ: 1.
Задание №2.
Решение:
.
Таким
образом
,
откуда
.
Задание №3.
Решение:
Пусть
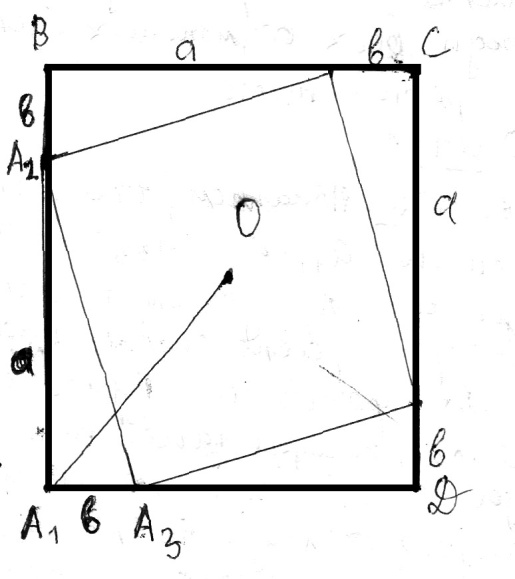
Достроим чертеж следующим образом (
-
данный треугольник). Получили квадрат
,
где
- искомое расстояние.
Ответ:
.
Задание №4.
Решение: Обозначим стертое число через . Так как -1 — корень, то
Получаем уравнение
или
Решим второе уравнение.
Ответ:
.
Задание №5.
Решение:
Обозначим точку O пересечения прямых.
Отметим на прямых точки
лежащие на расстоянии 1 от точки O.
Покажем, что ломаная
—
искомое гмт. Пусть точка
,
x- расстояние от
до
,
-
расстояние от
до
.
Муниципальный этап 2011-2012 учебный год
10 Класс
Задача № 1. В контрольной работе 20 задач. За каждую правильно решённую задачу ученик получает 8 баллов, за каждую неверно решённую – минус 5 баллов, за задачу, которую он не брался решать – 0 баллов. Ученик получил в сумме 13 баллов. Сколько задач он решил правильно и сколько неверно?
Задача № 2. В угол с вершиной А величиной α градусов вписана окружность радиуса r, которая касается сторон угла в точках В и С. Найдите радиус окружности, вписанной в треугольник АВС.
Задача № 3. Существует ли квадратный трёхчлен f(x) c целыми коэффициентами такой, что f(2010)=19, f(2011)=11, f(2012)=2011?
Задача № 4.
Пусть 
-- различные натуральные числа большие
1. Докажите, что 
.
Задача № 5. Рассмотрим множество всех десятизначных чисел, состоящих только из цифр 2 или 5. Сколько в этом множестве чисел, у которых две двойки не стоят рядом?