§ 2. Решение систем линейных уравнений
1. О системах линейных уравнений.
Многие задачи практики приводят к необходимости решать системы линейных уравнений. При конструировании инженерных сооружений, обработке результатов измерений, решении задач планирования производственного процесса и ряда других задач техники, экономики, научного эксперимента приходится решать системы линейных уравнений.
2. Решение систем линейных уравнений с двумя неизвестными по формулам Крамера.
Пусть дана система линейных уравнений с двумя неизвестными:
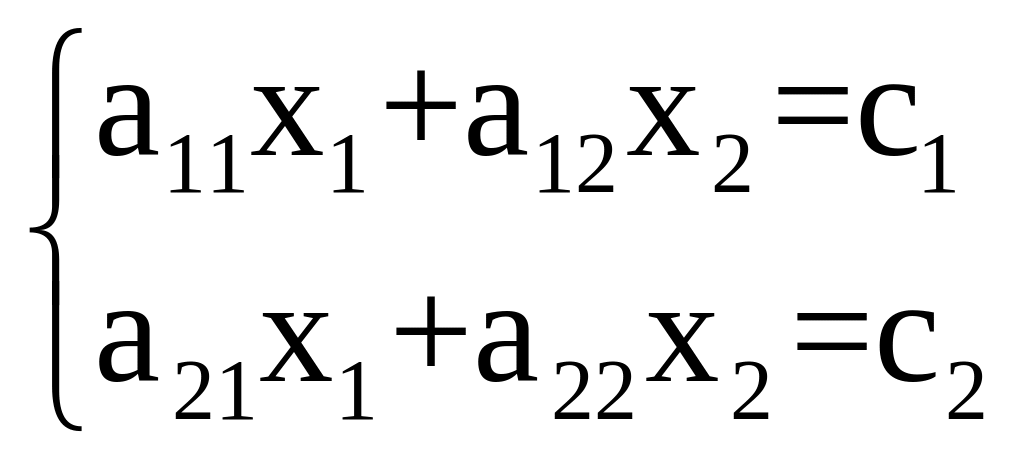(2.1)
Рассмотрим решение систем линейных уравнений с двумя и тремя неизвестными по формулам Крамера.
Теорема
1. Если главный определитель системы
отличен от нуля, то система имеет решение,
притом единственное. Решение системы
определяется формулами:
,
(2.2)
где x1, x2 - корни системы уравнений, – главный определитель системы, x1, x2 - вспомогательные определители.
Главный определитель системы определяется:
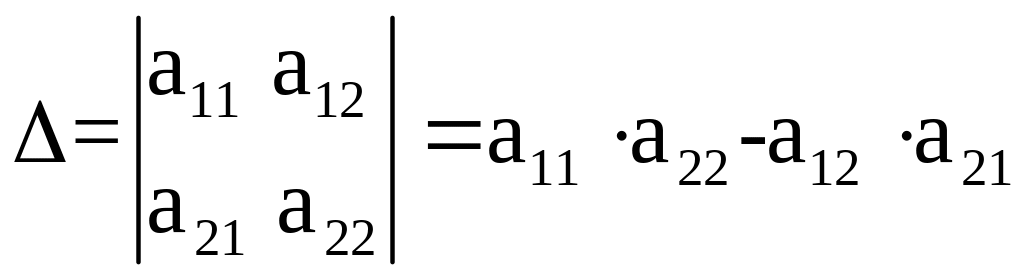
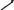
Вспомогательные определители:
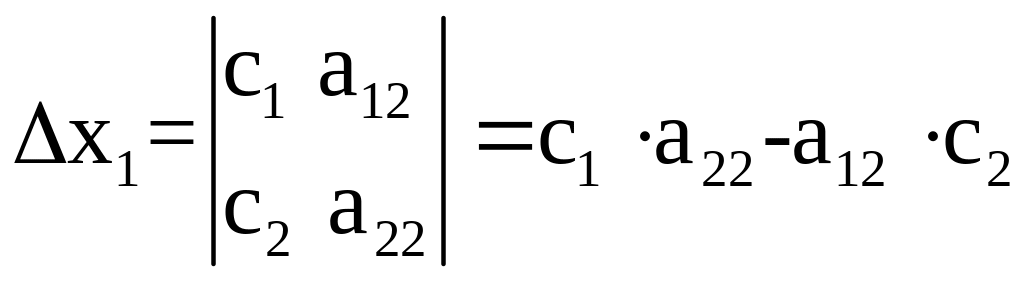
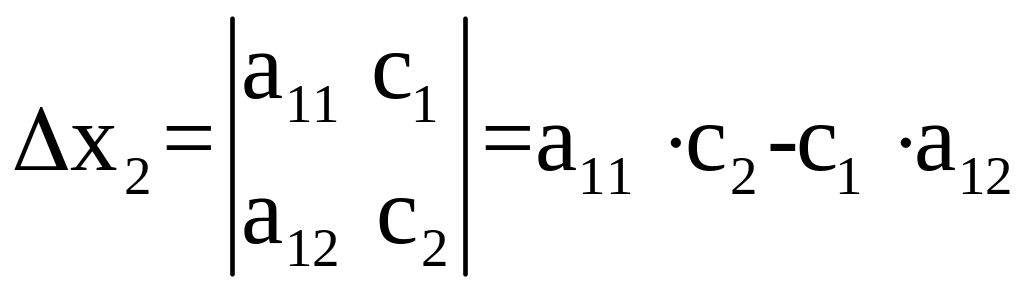
Пример 1.
Решить
систему уравнений по формулам Крамера:
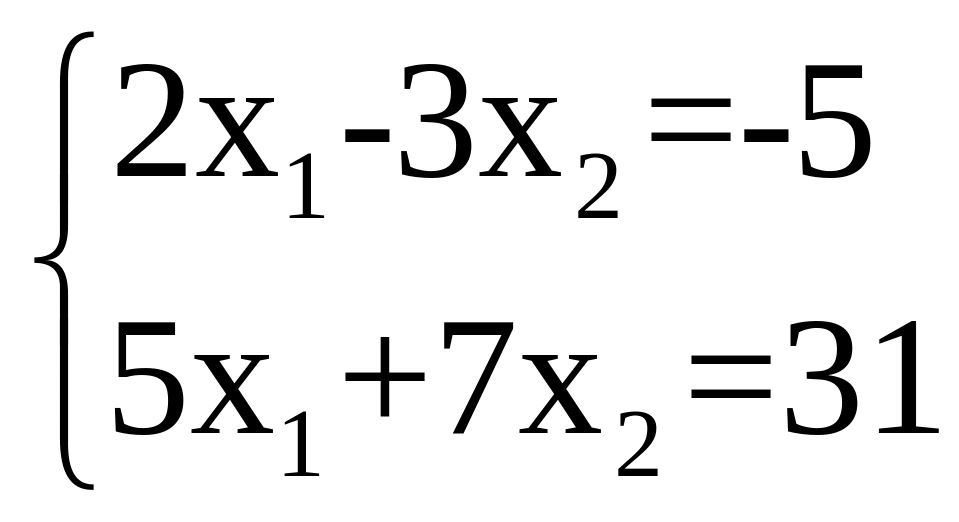
Решение:
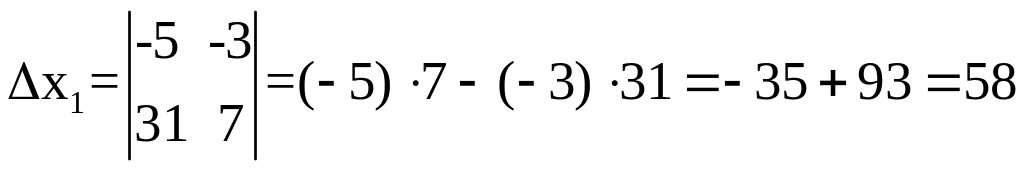
Ответ: x1=2; x2=3
{Программа 2.1}
program korni1; {Метод Крамера для системы }
label Out; {уравнений с двумя неизвестными}
var a: array[1..2,1..3] of integer;
x,y,dx,dy,d:real; i,j:integer;
begin
for i:=1 to 2 do
for j:=1 to 3 do readln(a[i,j]);
d:=a[1,1]*a[2,2]-a[2,1]*a[1,2];
if d=0 then begin
writeln('Единственого решения нет'); goto Out; end;
dx:=a[1,3]*a[2,2]-a[2,3]*a[1,2];
dy:=a[1,1]*a[2,3]-a[2,1]*a[1,3];
x:=dx/d; y:=dy/d;
writeln('x=',x); writeln('y=',y);
Out: end.
3. Решение систем линейных уравнений с тремя неизвестными по методу Крамера.
Пусть дана система линейных уравнений с тремя неизвестными:
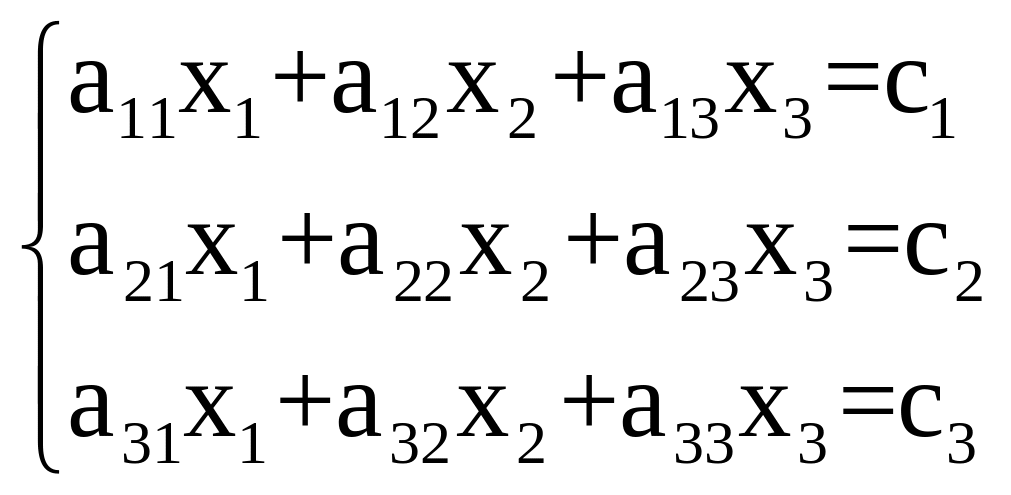(2.3)
Теорема
2. Если главный определитель системы
отличен от нуля, то система имеет решение,
притом единственное. Решение системы
определяется формулами:
,
,
,
(2.4)
где x1, x2, x3 - корни системы уравнений, - главный определитель системы, x1, x2, x3 - вспомогательные определители.
Главный определитель системы определяется:
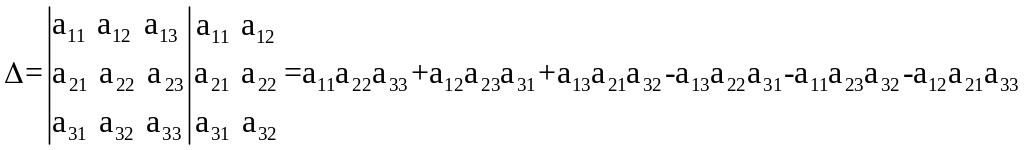
Вспомогательные определители:
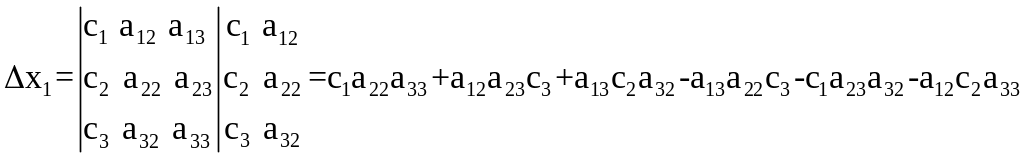
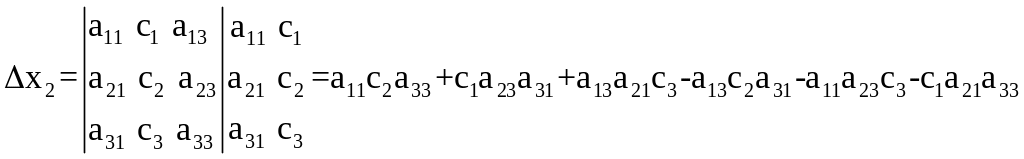
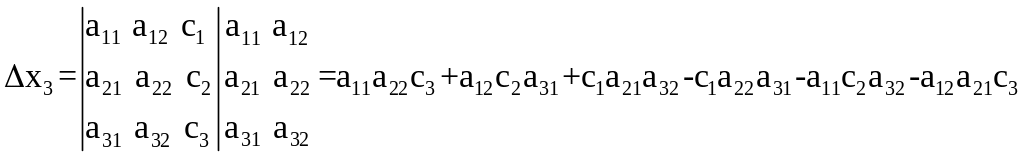
Пример 2. Решить систему уравнений по формулам Крамера.
Решение.
,
,
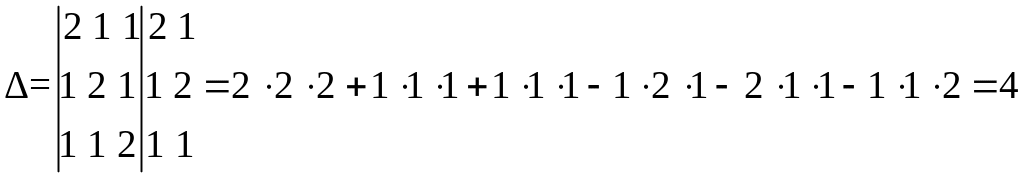
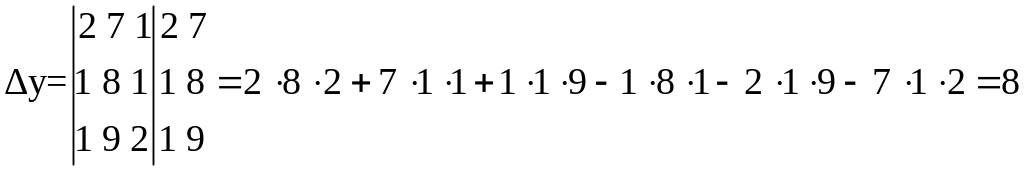
Ответ: x=1, y=2, z=3.
{Программа 2.2}
program korni2; {Метод Крамера для системы }
label Out; {уравнений с тремя неизвестными}
var a:array[1..3,1..4] of integer;
d1,d2,x,y,z,dx,dy,d,dz:real; i,j:integer;
begin
for i:=1 to 3 do begin
for j:=1 to 4 do read(a[i,j]); readln; end;
d1:=a[1,1]*a[2,2]*a[3,3]+a[1,2]*a[2,3]*a[3,1]+a[1,3]*a[2,1]*a[3,2];
d2:=a[3,1]*a[2,2]*a[1,3]+a[3,2]*a[2,3]*a[1,1]+a[3,3]*a[2,1]*a[1,2];
d:=d1-d2;
if d=0 then begin
writeln('Единственого решения нет');
goto Out;
end;
d1:=a[1,4]*a[2,2]*a[3,3]+a[1,2]*a[2,3]*a[3,4]+a[1,3]*a[2,4]*a[3,2];
d2:=a[3,4]*a[2,2]*a[1,3]+a[3,2]*a[2,3]*a[1,4]+a[3,3]*a[2,4]*a[1,2];
dx:=d1-d2;
d1:=a[1,1]*a[2,4]*a[3,3]+a[1,4]*a[2,3]*a[3,1]+a[1,3]*a[2,1]*a[3,4];
d2:=a[3,1]*a[2,4]*a[1,3]+a[3,4]*a[2,3]*a[1,1]+a[3,3]*a[2,1]*a[1,4];
dy:=d1-d2;
d1:=a[1,1]*a[2,2]*a[3,4]+a[1,2]*a[2,4]*a[3,1]+a[1,4]*a[2,1]*a[3,2];
d2:=a[3,1]*a[2,2]*a[1,4]+a[3,2]*a[2,4]*a[1,1]+a[3,4]*a[2,1]*a[1,2];
dz:=d1-d2;
x:=dx/d; y:=dy/d; z:=dz/d;
writeln('x=',x);
writeln('y=',y);
writeln('z=',z);
Out: end.