Основные положения симплекс-метода

Для аналитического решения задач линейного программирования разработан специальный алгоритм направленного перебора вершин ОРД (области допустимых решений). Этот алгоритм обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается. В геометрии есть такое понятие, как «симплекс». Симплексом тел в К-мерном пространстве называется совокупность (К+1) его вершин. Так, для плоскости при К=2 симплексом будут 3 вершины треугольника. При К=3 – 4 вершины четырехгранника и т.д. С учетом этого понятия аналитический метод решения задач линейного программирования называется симплекс-метод. Вычисления, обеспечивающие определение значения ЦФ и переменных в одной вершине называются итерацией.

5. Решение задач линейного программирования с помощью ms Excel Пример 1

Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, наличие располагаемого ресурса, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице:

	A	B	C	D	E	F	G
	Ресурс	Прод1	Прод2	Прод3	Прод4	знак	Наличие
	Прибыль	60	70	120	130	max	—
	Трудовые	1	1	1	1	<=	16
	Сырье	6	5	4	3	<=	110
	Финансы	4	6	10	13	<=	100

Решение:

1. Составим математическую модель, для чего введем следующие обозначения:

x_j – количество выпускаемой продукции j-ого типа, j=1, 2, 3,4;

b_i – количество располагаемого ресурса i -ого вида, i =1, 2, 3;

a_ij – норма расхода i -ого ресурса для выпуска единицы продукции j-ого типа;

c_j – прибыль, получаемая от реализации единицы продукции j-ого типа.

Для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 6х₁ единиц сырья, где х₁ – количество выпускаемой продукции Прод1. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид: 6х₁+5х₂+4х₃+3х₄110.

В этом ограничении левая часть равна величине потребного ресурса, а правая показывает количество имеющего ресурса.

Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:

(7.11)

2. Создание формы для ввода условий задачи. Для данной задачи создать форму для ввода как на рис 7.7. Весь текст на этом рисунке является комментариями, и на решение задачи не повлияет.

	A	B	C		D		E		F	G	H
1		Переменные
2	Имя	Прод1		Прод2		Прод3		Прод4
3	Значение
4	Нижн. гр.
5	Верх. гр.								ЦФ	Направление
6	Коэф. в ЦФ
7		Ограничения
8	Вид ресурсов								Лев. часть	Знак	Прав. часть
9	Трудовые
10	Сырье
11	Финансы

Рис 7.7

3. Ввод исходных данных. Ввести исходные данные в форму согласно условию задачи (Рис 7.8).

	A	B	C		D		E		F	G	H
1		Переменные
2	Имя	Прод1		Прод2		Прод3		Прод4
3	Значение
4	Нижн. гр.	0		0		0		0
5	Верх. гр.								ЦФ	Напр
6	Коэф. в ЦФ	60		70		120		130	0	макс
7		Ограничения
8	Вид ресурсов								Лев. часть	Знак	Прав. часть
9	Трудовые	1		1		1		1	0	<=	16
10	Сырье	6		5		4		3	0	<=	110
11	Финансы	4		6		10		13	0	<=	100

Рис 7.8

4. Ввод зависимостей из математической модели. Ввести зависимости из математической модели (7.11). В режиме представления формул это будет выглядеть как на рис 7.9

	A	B	C	D	E	F	G	H
1		Переменные
2	Имя	Прод1	Прод2	Прод3	Прод4
3	Значение
4	Нижн. гр.	0	0	0	0
5	Верх. гр.					ЦФ	Напр
6	Коэф. в ЦФ	60	70	120	130	=СУММПРОИЗВ(B$3:E$3;B6:E6)
7
8	Вид ресурсов	Ограничения				Лев. часть	Знак	Прав. часть
9	Трудовые	1	1	1	1	=СУММПРОИЗВ(B$3:E$3;B9:E9)	<=	16
10	Сырье	6	5	4	3	=СУММПРОИЗВ(B$3:E$3;B10:E10)	<=	110
11	Финансы	4	6	10	13	=СУММПРОИЗВ(B$3:E$3;B11:E11)	<=	100

Рис 7.9

5. Назначение целевой функции, ввод ограничений и граничных условий. Вызвать диалоговое окно Поиск Решения: Сервис-Поиск решения… (рис 7.10)

Рис 7.10

Назначить целевую функцию: $F$6

Ввести адреса искомых переменных: $B$3:$E$3

Ввести ограничения, нажав кнопку Добавить. Появиться диалоговое окно Добавление ограничения (рис 7.11)

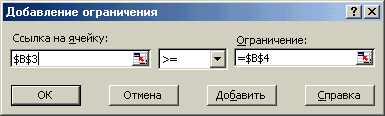
Рис 7.11

Ввести граничные условия: $B$3:$E$3$B$4:$E$4

Ввести ограничения: $F$9:$F$11$H$9:$H$11