Упражнения с решениями
Пример. Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга?
Решение.
Если радиус шара 
(рис. 11), то радиус круга в сечении будет
.
Отношение площади этого круга к площади
большого круга равно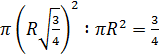 
.
Рисунок 11
Задания к практической работе
Задание 1. Шар, радиус которого 41 дм, пересечен плоскостью на расстоянии 9 дм от центра. Найдите площадь сечения.
Задание 2. Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга?
Задание 3. Радиус земного шара R. Чему равна длина параллели, если ее широта (рис. 12)?
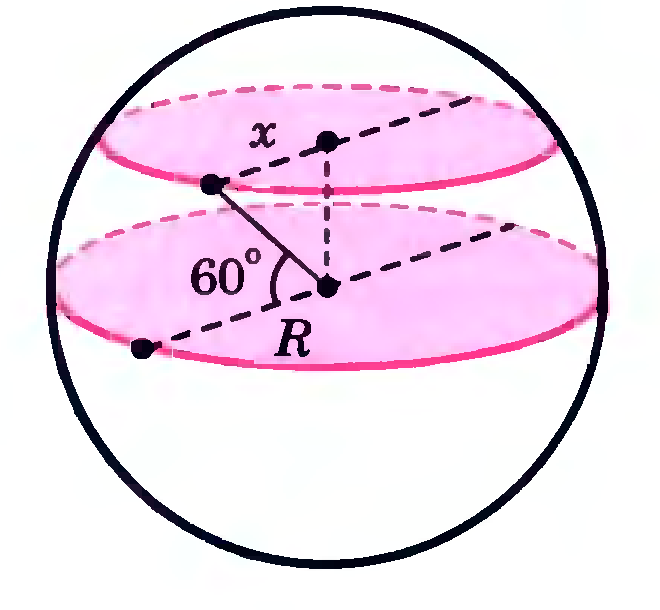
Рисунок 12
Задание 4. На поверхности шара даны три точки. Прямолинейные расстояния между ними 6 см, 8 см, 10 см. Радиус шара 13 см. Найдите расстояние от центра до плоскости, проходящей через эти точки.
Контрольные вопросы
Дайте определение шара.
Дайте определение сферы.
Докажите теорему 5 из теоретического материала данной практической работы.
Рекомендуемая литература: 1.2, 2.2
Практическая работа №53
Тема: Касательная плоскость к сфере
Цель: формирование навыков построения и нахождения касательной плоскости к сфере
Вид работы: индивидуальный
Время выполнения: 4 часа
Теоретический материал
Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы - большой окружностью.
Теорема 6. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания (рис. 13).
Рисунок 13
Теорема 7. Касательная плоскость имеет с шаром только одну общую точку - точку касания.
Прямая, проходящая через точку А шаровой поверхности перпендикулярно к радиусу, проведенному в эту точку, называется касательной (рис. 13).
Теорема 8. Через любую точку шаровой поверхности проходит бесконечно много касательных, причем все они лежат в касательной плоскости шара.
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Задания к практической работе
Задание 1. Дан шар радиуса. Через точку его поверхности проведены две плоскости: первая – касательная к шару, вторая под углом к первой. Найдите площадь сечения.
Задание 2. Тело ограничено двумя концентрическими шаровыми поверхностями (полый шар). Докажите, что его сечение плоскостью, проходящей через центр, равновелико сечению, касательному к внутренней шаровой поверхности (рис. 14).
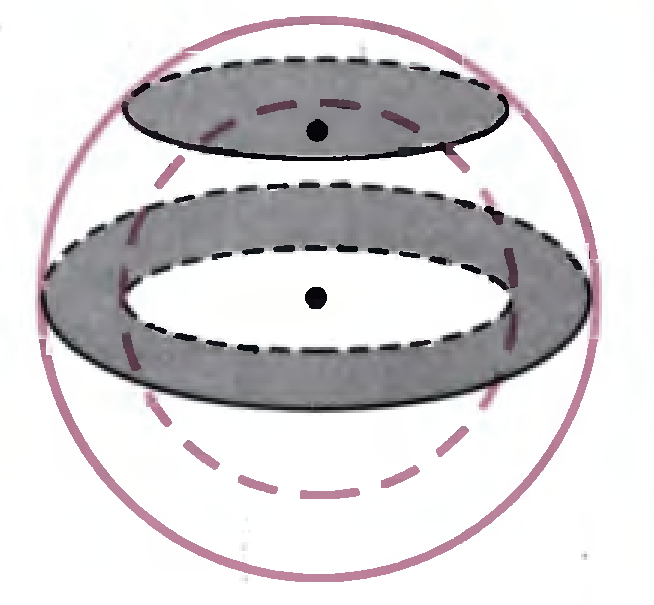
Рисунок 14
Задание 3. Стороны треугольника 13 см, 14 см и 15 см. Найдите расстояние от плоскости треугольника до центра шара, касающегося всех сторон треугольника. Радиус шара 5 см.
Задание 4. Диагонали ромба 15 см и 20 см. Шаровая поверхность касается всех его сторон. Радиус шара 10 см. Найдите расстояние от центра шара до плоскости ромба.
Задание 5. Шар радиуса R вписан в усеченный конус. Угол наклона образующей к плоскости нижнего основания конуса равен . Найдите радиусы оснований и образующую усеченного конуса.