Задания к практической работе

Задание 1. Докажите, что в наклонной треугольной призме расстояние от бокового ребра до противоположной грани равно высоте треугольника, который служит перпендикулярным сечением призмы.

Задание 2. Основанием прямой призмы служит ромб; диагонали призмы и высота соответственно равны 8, 5 и 2 см. Вычислите сторону основания призмы.

Задание 3. Вычислите угол между диагональю куба и его основанием.

Задание 4. Какой длины нужно взять проволоку для изготовления каркаса куба со всеми его диагоналями, если ребро куба равно 10 см?

Задание 5. Грани параллелепипеда – равные ромбы со стороной а и углом . Вычислите площади его диагональных сечений.

Контрольные вопросы

1. Что называется призмой? Какие виды вы знаете?

2. Что называется высотой призмы?

3. Что называется сечением призмы?

4. Какая фигура называется параллелепипедом?

5. Что называется кубом?

Рекомендуемая литература: 1.2, 2.2

Практическая работа №48

Тема: Пирамида: правильная, усеченная

Цель: формирование навыков нахождения основных характеристик пирамиды и усеченной пирамиды

Вид работы: индивидуальный

Время выполнения: 4 часа

Теоретический материал

Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания - вершины пирамиды и всех отрезков, соединяющих вершину с точками основания (рис. 3). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. На рисунке 3, а изображена пирамида SABCD. Четырехугольник АВСD - основание пирамиды, точка S - вершина пирамиды, отрезки SА, SВ, SС и SD - ребра пирамиды.

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. На рисунке 3, а SO - высота пирамиды.

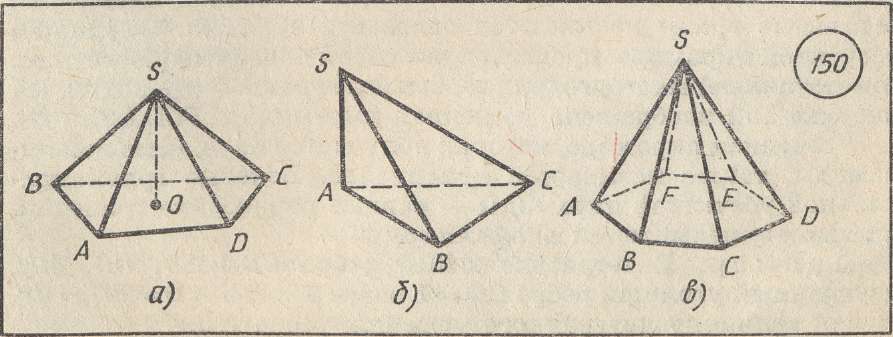
Рисунок 3

Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром.

На рисунке 4, а изображена треугольная пирамида, или тетраэдр, на рисунке 4, б – четырехугольная, на рисунке 4, в – шестиугольная.

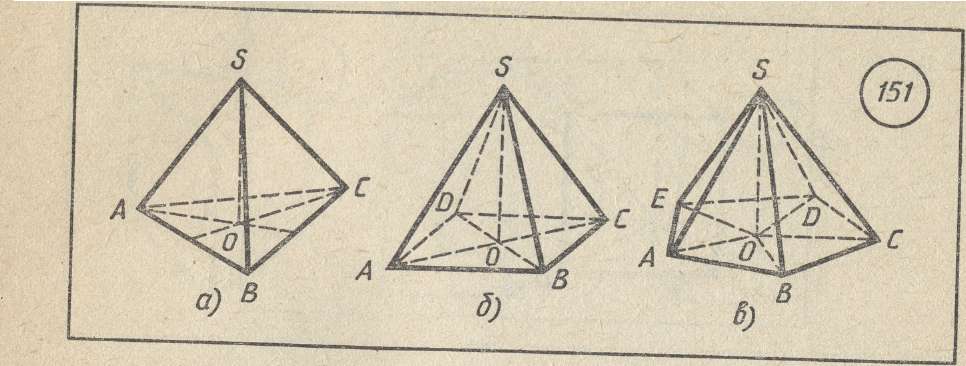
Рисунок 4

Теорема 4. Плоскость, параллельная основанию пирамиды и пересекающая ее, отсекает подобную пирамиду.

Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.

По теореме 4 плоскость , параллельная плоскости основания пирамиды и пересекающая пирамиду, отсекает от нее подобную пирамиду. Другая часть пирамиды представляет собой многогранник, который называется усеченной пирамидой (рис. 5).

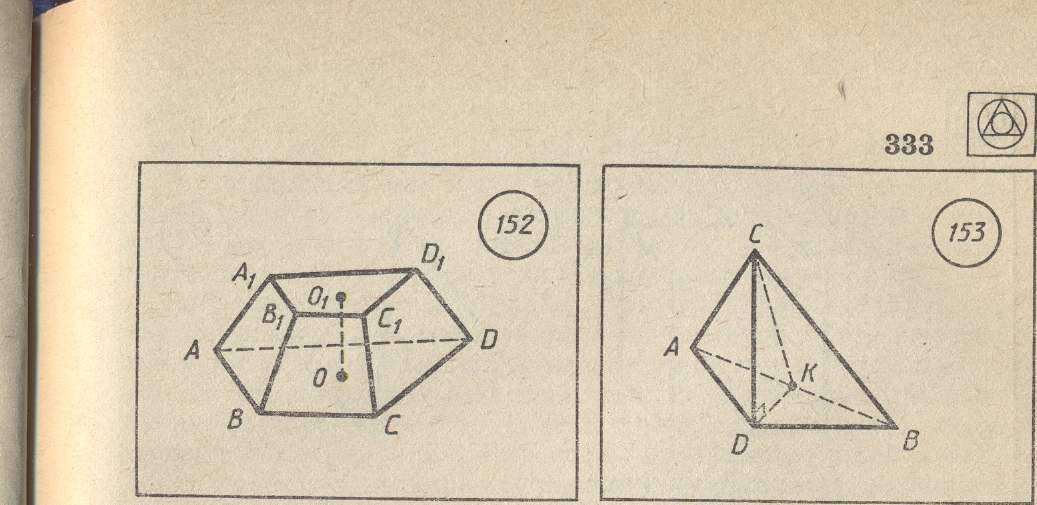
Рисунок 5

Усеченная пирамида, которая получается из правильной пирамиды также называется правильной.

Упражнения с решениями

Пример. В тетраэдре АВСD ребро , двугранный угол при ребре СD = 1 равен 120°, а . Найти величину двугранного угла при ребре АВ.

Решение. Пусть К - середина ребра АВ (рис. 6). Отрезок СD перпендикулярен двум пересекающимся прямым ВD и АD плоскости АВD, а значит, ребро СD перпендикулярно плоскости АВD, откуда ABD=120°. КD - медиана равнобедренного треугольника АDВ, а значит, и его высота, КD АВ. Следовательно, КC АВ, а тогда CKD - линейный угол двугранного угла при ребре АВ. Не­трудно найти его величину (сделайте это самостоятельно). Ответ: CKD= 45°.

Рисунок 6