Контрольные вопросы

1. Дайте определение случайной величины.

2. Какие виды случайных величин вы знаете? Приведите примеры.

3. Что называется генеральной совокупностью?

4. Что называется выборкой?

5. Дайте определение моды, медианы и среднего арифметического.

6. Как вычислить математическое ожидание случайной величины?

7. Дайте определение отклонения от среднего.

8. Что называется дисперсией?

9. Как вычислить дисперсию?

10. Дайте определение среднего квадратичного отклонения.

Рекомендуемая литература: 1.1, 1.3, 2.1

Практическая работа №44

Тема: Прямые и плоскости в пространстве

Цель: формирование навыков решения задач на доказательство существования прямых и плоскостей, используя основные аксиомы стереометрии

Вид работы: индивидуальный

Время выполнения: 6 часов

Теоретический материал

Основными геометрическими фигурами в пространстве являются точка, прямая и плоскость.

Плоскости обозначаются строчными греческими буквами:

Перечислим аксиомы, которые выражают основные свойства плоскостей в пространстве

C₁: Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

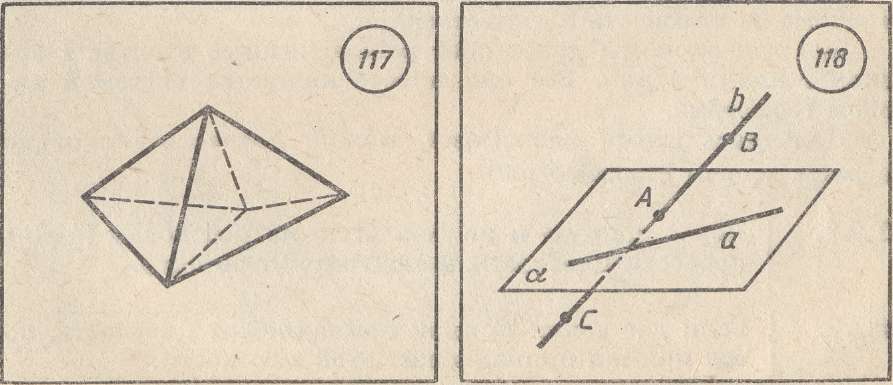
Рисунок 2

На рисунке 2 точка А принадлежит плоскости , а точки B и С не принадлежат ей.

C₂: Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

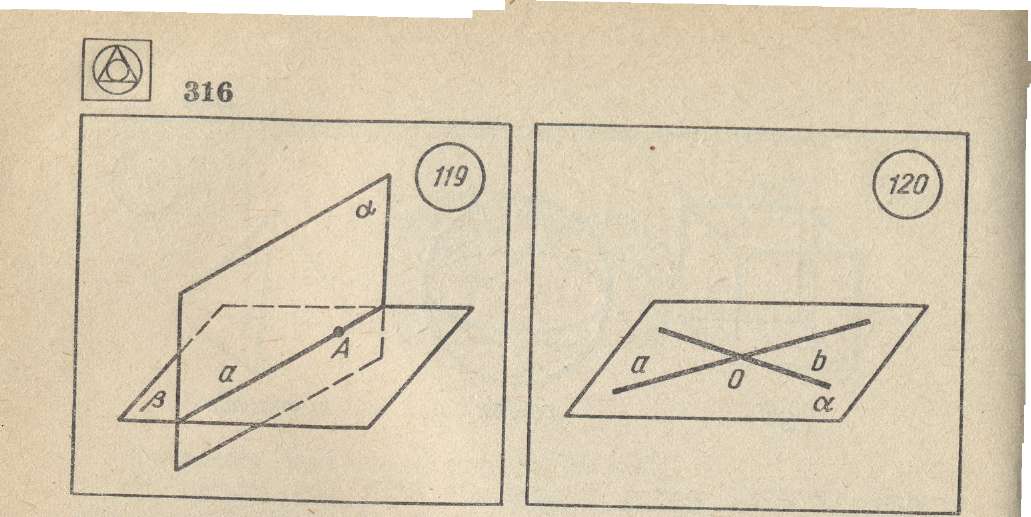
Рисунок 3

На рисунке 3 две различные плоскости и имеют общую точку А, а значит, по аксиоме С₂ существует прямая принадлежащая каждой из этих плоскостей. При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой а.

Плоскости и в этом случае называются пересекающимися по прямой а.

C₃: Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Рисунок 4

На рисунке 4 изображены две различные прямые a и b имеющие общую точку О, а значит, по аксиоме С₃, существует плоскость , содержащая прямые a и b. При этом по той же аксиоме C₃ плоскость единственная.

Пользуясь этими аксиомами, можно доказать несколько первых теорем стереометрии.

Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

Теорема 2. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Теорема 3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Упражнения с решениями

Пример 1. Дана плоскость . Доказать, что существует прямая, не лежащая в плоскости и пересекающая ее.

Решение. Возьмем в плоскости точку А, что можно сделать по аксиоме С₁. По той же аксиоме существует точка В, которая плоскости не принадлежит. Через точки А и В можно провести прямую. Прямая АВ не лежит в плоскости и пересекает ее (в точке А).

Пример 2. Дана плоскость . Доказать, что существует другая плоскость , пересекающая .

Решение. Возьмем точки А и В, принадлежащие плоскости , и точку С, не принадлежащую ей (аксиома С₁). Точки А, В и С не лежат на одной прямой. Через них по теореме 3 можно провести плоскость , и притом только одну. Плоскости и имеют общую точку, а значит, по аксиоме С₂ плоскости и пересекаются.