
- •Министерство образования и науки российской федерации
- •230115 Программирование в компьютерных системах
- •230401 Информационные системы (по отраслям)
- •Пояснительная записка
- •Общие требования к выполнению практических занятий:
- •Критерии оценки практических работ
- •Практическая работа№34
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №35
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №38
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы:
- •Практическая работа №39
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №41
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы:
- •Список литературы
- •1. Основная:
- •2. Дополнительная:
Упражнения с решениями
Пример 1. Найти площадь криволинейной трапеции, изображенной на рисунке 11.
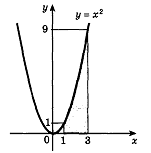
Рис. 11
Решение.
По формуле (3) находим  .
Вычислим этот интеграл с помощью формулы
Ньютона-Лейбница (2). Одной из первообразных
функции
является
.
Поэтому
.
Вычислим этот интеграл с помощью формулы
Ньютона-Лейбница (2). Одной из первообразных
функции
является
.
Поэтому 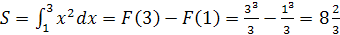 (кв.ед).
(кв.ед).
Пример 2.
Найти площадь фигуры, ограниченной
параболами  и
и  .
.
Решение.
Построим данную фигуру (рис. 12) и найдем
абсциссы точек пересечения парабол из
уравнения ![]() .
.
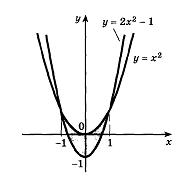
Рис. 12
Это уравнение
имеет корни ![]() .
Воспользуемся формулой (5). Здесь
.
Воспользуемся формулой (5). Здесь ![]() ,
,
![]() .
.

Задания к практическому занятию
Задание 1.
Найти площадь криволинейной трапеции,
ограниченной прямыми ![]() ,
осью
и графиком функции
:
,
осью
и графиком функции
:
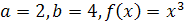 ;
;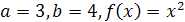 ;
; ;
; ;
;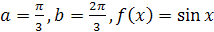 ;
;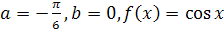 .
.
Задание 2. Найти площадь фигуры, ограниченной осью и параболой:
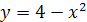 ;
; ;
; .
.
Задание 3. Найти площадь фигуры, ограниченной прямой , осью и графиком функции :
 ;
; ;
;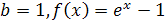 ;
;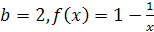 .
.
Задание 4. Найти площадь фигуры, ограниченной заданными линиями:
Параболой
 ,
прямой
,
прямой 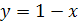 и осью
;
и осью
;Параболой , прямой
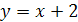 и осью
;
и осью
;Графиками функций
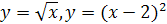 и осью
;
и осью
;Параболой
 и прямой
и прямой  ;
;Параболой
 и прямой
;
и прямой
;Параболой
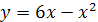 и прямой
и прямой  ;
;Параболой и прямой ;
Параболой и прямой, проходящей через точки
 и
и 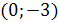 ;
;Графиком функции
 и прямыми
и прямыми  .
.
Задание 5.
Фигура ограничена линиями ![]() .
Найти точку
.
Найти точку ![]() графика функции
графика функции ![]() ,
через которую надо провести касательную
к этому графику так, чтобы она отсекала
от фигуры трапецию наибольшей площади.
,
через которую надо провести касательную
к этому графику так, чтобы она отсекала
от фигуры трапецию наибольшей площади.
Контрольные вопросы
Дайте определение криволинейной трапеции.
По каким формулам можно вычислить площадь криволинейных трапеций?
Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1
Практическая работа №41
Тема: Решение задач на подсчет числа размещений, перестановок, сочетаний
Цель: формирование навыков решения задач на подсчет числа размещений, перестановок, сочетаний
Вид работы: индивидуальный
Время выполнения: 14 часов
Теоретический материал
Перестановками
из ![]() элементов
называются соединения, которые состоят
из одних и тех же
элементов и отличаются одно от другого
только порядком их расположения.
элементов
называются соединения, которые состоят
из одних и тех же
элементов и отличаются одно от другого
только порядком их расположения.
Число перестановок
из
элементов
обозначают
![]() и читают
«пэ энное». Формула числа перестановок
из
различных элементов:
и читают
«пэ энное». Формула числа перестановок
из
различных элементов:
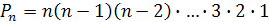 ,
,
![]() .
.
Произведение
первых
натуральных чисел обозначают
![]() (читается
«эн факториал»), т. е.
(читается
«эн факториал»), т. е.  ,
причём по определению
,
причём по определению 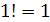 .
Таким образом,
.
Таким образом,
 (1)
(1)
Размещениями
из ![]() элементов по
элементов (
элементов по
элементов (![]() )
называются такие соединения, каждое
из которых содержит
элементов, взятых из данных
разных элементов, и которые отличаются
одно от другого либо самими элементами,
либо порядком их расположения.
)
называются такие соединения, каждое
из которых содержит
элементов, взятых из данных
разных элементов, и которые отличаются
одно от другого либо самими элементами,
либо порядком их расположения.
Число всевозможных
размещений из
элементов по
элементов обозначают 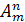 и читают «А
из эм по эн».
и читают «А
из эм по эн».
Формула для вычисления - числа размещений из элементов по элементов имеет следующий вид:
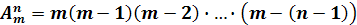 (2)
(2)
Например,  .
.
Отметим, что правая
часть формулы (2) содержит произведение
последовательных натуральных чисел,
наибольшее из которых равно
.
Пусть в формуле (2)
![]() .
Тогда
.
Тогда

т. е. число размещений из элементов по равно числу перестановок из этих элементов:
 (3)
(3)
Сочетаниями из элементов по в каждом ( ) называются соединения, каждое из которых содержит элементов, взятых из данных разных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Число всевозможных
сочетаний из
различных элементов по
элементов обозначают
![]() и читают «це из эм по эн».
и читают «це из эм по эн».
Формула для подсчёта числа сочетаний из различных элементов по элементов в каждом имеет следующий вид:
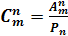 (4)
(4)
Рассмотрим свойства сочетаний, которые в ряде случаев упрощают вычисления при решении задач.
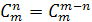 .
.Рекуррентное свойство
![]()
