Контрольные вопросы:

1. Что называют первообразной функции?

2. Что называют интегрированием?

3. Назовите обратную операцию нахождения первообразной функции.

4. Перечислите основные правила интегрирования.

Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1

Практическая работа №39

Тема: Вычисление определенного интеграла по формуле Ньютона-Лейбница

Цель: формирование навыков вычисления определенного интеграла при помощи формулы Ньютона – Лейбница

Вид работы: индивидуальный

Время выполнения: 4 часа

Теоретический материал

Функция, интегрируемая на промежутке , если при любых разбиениях промежутка , таких, что при произвольном выборе точек (где ), сумма при стремится к пределу .

Предел называют определенным интегралом от функции на промежутке и обозначают , то есть .

Число называется нижним пределом интеграла, - верхним. Промежуток называется промежутком интегрирования, - переменной интегрирования.

Для вычисления определенного интеграла от функции в том случае, когда можно найти соответствующий неопределенный интеграл , служит формула Ньютона – Лейбница: . То есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

Упражнения с решениями

Пример 1. Вычислить интеграл .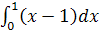

Решение. Одной из первообразных функции является функция . Поэтому .

Пример 2. Вычислить интеграл .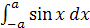

Решение. , так как .

Пример 3. Вычислить интеграл .

Решение. .

Задания к практическому занятию

Задание 1. Вычислить интеграл:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. ;

29. ;

30. .

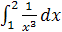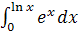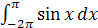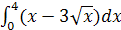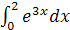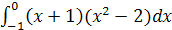Задание 2. Найдите все числа , для которых выполняется равенство .

Контрольные вопросы

1. Дайте определение определенного интеграла.

2. В чем заключается суть формулы Ньютона – Лейбница?

Рекомендуемая литература: 1.1, 1.4, 2.1

Практическая работа №40

Тема: Применение определенного интеграла для нахождения площади криволинейной трапеции

Цель: формирование навыков вычисления площади криволинейной трапеции с помощью определенного интеграла

Вид работы: индивидуальный

Время выполнения: 4 часа

Теоретический материал

Рассмотрим фигуру изображенную на рисунке 8. Эта фигура ограничена снизу отрезком оси , сверху графиком непрерывной функции такой, что при и при , а с боков ограничена отрезками прямых и . Такую фигуру называют криволинейной трапецией. Отрезок называют основанием этой криволинейной трапеции.

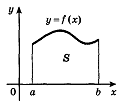
Рис. 8

Площадь криволинейной трапеции (рис. 8) можно вычислить по формуле

, (1)

Где – любая первообразная функции .

Таким образом, вычисление площади криволинейной трапеции сводится к отысканию первообразной функции , т.е. к интегрированию функции .

Разность называют интегралом от функции на отрезке и обозначают так : (читается: «Интеграл от до эф от икс дэ икс»), т.е.

(2)

Из формул (1) и (2) получаем

(3)

Если на отрезке , причем равенство нулю может быть лишь на его концах (рис.9), то площадь криволинейной трапеции равна

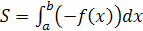(4)

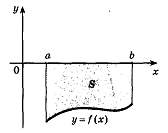
Рис. 9

Площадь фигуры, изображенной на рисунке 10 равна

(5)

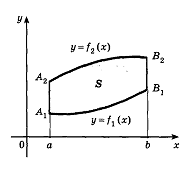
Рис. 10