
- •Министерство образования и науки российской федерации
- •230115 Программирование в компьютерных системах
- •230401 Информационные системы (по отраслям)
- •Пояснительная записка
- •Общие требования к выполнению практических занятий:
- •Критерии оценки практических работ
- •Практическая работа№34
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №35
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №38
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы:
- •Практическая работа №39
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №41
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы:
- •Список литературы
- •1. Основная:
- •2. Дополнительная:
Упражнения с решениями
Пример 1.
Исследовать на монотонность функцию
![]() .
.
Решение.
Имеем ![]() .
Справедливо неравенство
.
Справедливо неравенство ![]() ,
причем знак равенства имеет место лишь
в одной точке
.
Значит, функция
возрастает на всей числовой прямой.
,
причем знак равенства имеет место лишь
в одной точке
.
Значит, функция
возрастает на всей числовой прямой.
Пример 2.
Исследовать на экстремум функцию ![]() .
.
Решение. 1) Функция определена при всех .
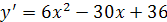 .
.Из уравнения
 находим
находим  .
.существует при всех .
Отметим точки на координатной прямой.
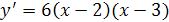 .
Отметим знаки производной на полученных
промежутках.
.
Отметим знаки производной на полученных
промежутках.При переходе через точку
 слева направо производная
меняет знак с «+» на «-», значит,
- точка максимума; при переходе через
точку
слева направо производная
меняет знак с «+» на «-», значит,
- точка максимума; при переходе через
точку  производная меняет знак с «-» на «+»,
значит,
- точка минимума. В точке
имеем
производная меняет знак с «-» на «+»,
значит,
- точка минимума. В точке
имеем 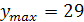 ,
в точке
имеем
,
в точке
имеем  .
.
Пример 3.
Построить график функции ![]() .
.
Решение.
1) Область определения – множество ![]() всех действительных чисел.
всех действительных чисел.
 .
.Решая уравнение
 ,
находим стационарные точки
,
находим стационарные точки  и
и  .
.Производная положительна на интервале
 ,
следовательно, на этом интервале
функция возрастает. На промежутках
,
следовательно, на этом интервале
функция возрастает. На промежутках
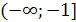 и
и  производная отрицательна, следовательно,
на этих промежутках функция убывает.
производная отрицательна, следовательно,
на этих промежутках функция убывает.Стационарная точка является точкой минимума, так как при переходе через эту точку производная меняет знак с «-» на «+»;
 .
Точка
– точка максимума, так как при переходе
через нее производная меняет знак с
«+» на «-»;
.
Точка
– точка максимума, так как при переходе
через нее производная меняет знак с
«+» на «-»;  .
.
Составим таблицу:
Таблица 1
-
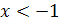
-1

0
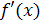
-
0
+
0
-
убывает
-0,5
возрастает
1
убывает
Используя результаты исследования, строим график функции (рис. 6).
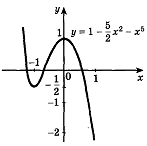
Рис. 6
Задания к практическому занятию
Задание 1. Найти промежутки возрастания и убывания функции:
 ;
; ;
; ;
; .
.
Задание 2.
При каких значениях ![]() функция возрастает на всей числовой
прямой:
функция возрастает на всей числовой
прямой:
 ;
; ?
?
Задание 3. Найти стационарные точки функции:
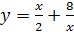 ;
;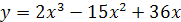 ;
;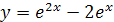 ;
; .
.
Задание 4. Найти точки экстремума функции:
 ;
;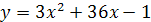 ;
; ;
;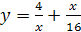 .
.
Задание 5. Построить график функции:
 ;
; ;
;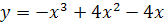 ;
; ;
; ;
; ;
;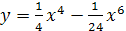 ;
; .
.
Задание 6. Построить график функции:
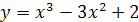 на отрезке
на отрезке  ;
; на отрезке
на отрезке  .
.
Задание 7.
На рисунке 7 изображен график функции
![]() ,
являющейся производной функции
.
Используя график, найти точки экстремума
функции
.
,
являющейся производной функции
.
Используя график, найти точки экстремума
функции
.
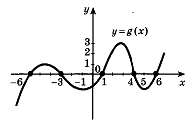
Рис. 7
Задание 8. Построить график функции:
 ;
; ;
; ;
; ;
; ;
; ;
;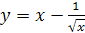 ;
;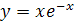 ;
;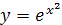 ;
;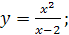
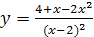 ;
; .
.
Задание 9. Найти число действительных корней уравнения:
 ;
;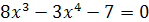 .
.
Задание 10.
Построить график функции ![]() .
Сколько действительных корней имеет
уравнение
.
Сколько действительных корней имеет
уравнение ![]() при различных значениях
при различных значениях ![]() ?
?
Задание 11. Найти наибольшее и наименьшее значения функции:
 на отрезке
на отрезке  .
.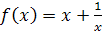 на отрезке
на отрезке  .
. на отрезке
на отрезке 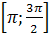 .
.
