Контрольные вопросы

1. Перечислите правила нахождения производной функции.

2. Чему равна производная суммы дифференцируемых функций?

3. Чему равна производная произведения дифференцируемых функций?

4. Чему равна производная частного двух дифференцируемых функций?

5. Чему равна производная постоянной величины и степенной функции?

6. Чему равна производная показательной и логарифмической функций?

7. Чему равны производные тригонометрических функций?

Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1

Практическая работа №36

Тема: Производная сложной функции

Цель: формирование навыков нахождения производной сложных функций

Вид работы: индивидуальный

Время выполнения: 4 часа

Теоретический материал

Пусть и - дифференцируемые функции. Тогда сложная функция есть также дифференцируемая функция, причем , или .

Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.

Упражнения с решениями

Пример. Найти производные следующих функций:

1) ;

2) ;

3) ;

4) ;

5) .

Решение: 1) , пусть . Таким образом, .

2) , перепишем данное выражение в виде . Получим, .

3) , пусть , получим . Тогда получим, .

4) , , что , , что .

5) , перепишем данное выражение в виде . Получим, .

Задания к практическому занятию

Задание. Найдите производные следующих функций:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) ;

13) ;

14) ;

15) ;

16) ;

17) ;

18) ;

19) ;

20) ;

21) ;

22) ;

23) .

Контрольные вопросы

1. Какая функция называется сложной?

2. По какой формуле находится производная сложной функции?

3. Чему равна производная сложной функции?

Рекомендуемая литература: 1.1, 1.3, 2.1

Практическая работа №37

Тема: Применение производной к исследованию функций и построению графиков

Цель: - формирование навыков нахождения промежутков возрастания и убывания функции;

- формирование навыков нахождения экстремумов функции;

- формирование навыков исследования функции с помощью производной;

- формирование навыков построения графиков функции.

Вид работы: индивидуальный

Время выполнения: 10 часов

Теоретический материал

1. Применение производной к исследованию функций на монотонность

Производная позволяет во многих случаях исследовать функцию на монотонность.

Если на промежутке, то функция возрастает на этом промежутке.

Если на промежутке, то функция убывает на этом промежутке.

2. Применение производной к исследованию функций на экстремум.

Точка называется точкой максимума функции , если существует такая окрестность точки , что для всех из этой окрестности выполняется неравенство .

Точка называется точкой минимума функции , если существует такая окрестность точки , что для всех из этой окрестности выполняется неравенство .

Точки минимума и точки максимума называются точками экстремума.

Теорема. Если - точка экстремума дифференцируемой функции , то .

Точки, в которых производная функции равна 0, называются стационарными.

Точки, в которых функция имеет производную, равную нулю, или недифференцируема, называют критическими точками этой функции.

Теорема. Пусть функция дифференцируема на интервале и . Тогда:

1. если при переходе через стационарную точку функции ее производная меняет знак с «плюса» на «минус», т.е. слева от точки и справа от точки , то - точка максимума функции (рис. 4);

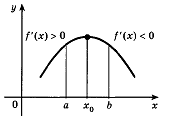
Рис. 4

2. если при переходе через стационарную точку функции ее производная меняет знак с «минус» на «плюса», то - точка минимума функции (рис. 5).

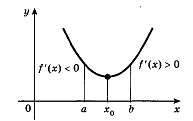
Рис. 5

Правило исследования функции на экстремум:

1. Найти область определения функции;

2. Найти ;

3. Найти точки, в которых выполняется равенство ;

4. Найти точки, в которых не существует;

5. Отметить на координатной прямой все критические точки и область определения функции ; получатся промежутки области определения функции, на каждом из которых производная функции сохраняет постоянный знак;

6. Определить знак на каждом из промежутков, полученных в п.5;

7. Сделать выводы о наличии или отсутствии экстремума в каждой из критических точек.

3. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке .

1. Найти .

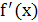2. Найти точки, в которых или не существует, и отобрать из них те, что лежат внутри отрезка .

3. Вычислить значения функции в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции на отрезке .

Пусть нужно построить график функции . Для этого нужно рассмотреть некоторые свойства функции.

При исследовании свойств функции полезно найти:

1. область её определения;

2. производную;

3. стационарные точки;

4. промежутки возрастания и убывания;

5. точки экстремума и значения функции в этих точках.

Результаты исследования удобно записать в виде таблицы. Затем, используя таблицу, строят график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и, быть может, еще несколько точек графика.

Для построения графика четной (нечетной) функции достаточно исследовать свойства и построить ее график при , а затем отобразить его симметрично относительно оси ординат (начала координат).