
- •Министерство образования и науки российской федерации
- •230115 Программирование в компьютерных системах
- •230401 Информационные системы (по отраслям)
- •Пояснительная записка
- •Общие требования к выполнению практических занятий:
- •Критерии оценки практических работ
- •Практическая работа№34
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №35
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №38
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы:
- •Практическая работа №39
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №41
- •Теоретический материал
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы:
- •Список литературы
- •1. Основная:
- •2. Дополнительная:
Контрольные вопросы
Что называют касательной к графику функции?
Что называется угловым коэффициентом прямой?
В чем заключается геометрический смысл производной?
Выведите уравнение касательной к графику дифференцируемой функции.
Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1
Практическая работа №35
Тема: Правила нахождения производной
Цель: формирование навыков нахождения производной функции по основным правилам дифференцирования
Вид работы: индивидуальный
Время выполнения: 6 часов
Теоретический материал
Введем обозначения:
![]() - постоянная;
- постоянная;
![]() - аргумент;
- аргумент;
![]() - функции от
,
имеющие производные.
- функции от
,
имеющие производные.
Основные правила дифференцирования
Производная алгебраической суммы функций:
![]() .
.
Производная произведения двух функций:
![]() .
.
Производная произведения трех функций:
![]() .
.
Производная произведения постоянной величины на функцию:
![]() .
.
Производная частного (дроби):
![]() .
.
Частные случаи дроби:
![]() ;
; ![]() .
.
При вычислении
производных необходимо помнить, что
![]() ;
;
![]() ;
;
![]() ,
и знать следующие правила действий со
степенями и корнями:
,
и знать следующие правила действий со
степенями и корнями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
 .
.
Здесь
![]() и
и
![]() - любые рациональные числа.
- любые рациональные числа.
Запишем основные правила дифференцирования, формулы производных основных элементарных функций запишем в виде таблицы.
На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведенной ниже таблице формул дифференцирования аргумент «х» заменен на промежуточный аргумент «u».
Правила дифференцирования
 ;
; ,
в частности
,
в частности  ;
; ,
в частности
,
в частности 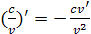 ;
; ,
если
,
если 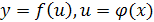 ;
; ,
если
,
если  .
.
Формулы дифференцирования:
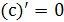 ;
; ,
в частности
,
в частности 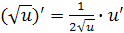 ;
; ,
в частности
,
в частности  ;
; ,
в частности
,
в частности 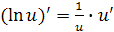 ;
; ;
; ;
; ;
; ;
; ;
; ;
;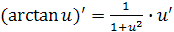 ;
; .
.
Упражнения с решениями
Пример 1.
Найти ![]() ,
если
,
если ![]()
Решение:
![]() .
.
Пример 2.
Найти производную функции ![]() ,
если
,
если ![]() ,
,
![]() .
.
Решение:
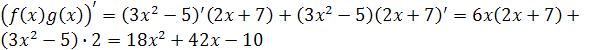 .
.
Пример 3.
Найти производную функции ![]() .
.
Решение: Обозначим
![]() .
.
![]() .
.
Задания к практическому занятию
Задание 1. Найти производную функции:
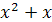 ;
; ;
;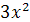 ;
; ;
;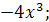
 ;
; ;
;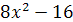 ;
; ;
; ;
; ;
;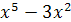 ;
; ;
; ;
; ;
; .
.
Задание 2.
Построить график функции ![]() и график функции, являющейся ее
производной.
и график функции, являющейся ее
производной.
Задание 3. Найти производную функции:
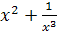 ;
;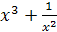 ;
; ;
; .
.
Задание 4.
Найти ![]() и
и ![]() ,
если:
,
если:
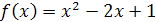 ;
; ;
;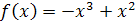 ;
;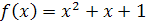 .
.
Задание 5.
Найти ![]() и
и ![]() ,
если:
,
если:
 ;
; ;
; ;
; .
.
Задание 6.
Найти значения ![]() ,
при которых значение производной
функции
,
при которых значение производной
функции ![]() равно 0, если:
равно 0, если:
;
 ;
; ;
; ;
; ;
; .
.
Задание 7. Найти производную функции:
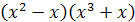 ;
; ;
; .
.
Задание 8. Найти , если:
 ;
;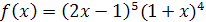 ;
; ;
; .
.
Задание 9.
Пересекается ли график функции,
являющийся производной функции ![]() ,
с графиком функции
,
с графиком функции ![]() ?
?
Задание 10.
При каких значениях
значение производной функции ![]() равно 0?
равно 0?
Задание 11. Найти производную функции:
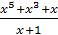 ;
; .
.
Задание 12. Найти , если:
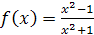 ;
;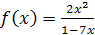 .
.
Задание 13.
При каких значениях
значение производной функции ![]() равно 0?
равно 0?
Задание 14.
При каких значениях
значение производной функции ![]() равно 3?
равно 3?
Задание 15.
При каких значениях
значение производной функции ![]() равно 11?
равно 11?
Задание 16. При каких значениях производная функции принимает положительные значения:
 ;
; ;
; ;
; .
.
Задание 17. При каких значениях производная функции принимает отрицательные значения:
 ;
; ;
; ;
; .
.
