Теоретический материал

Число называется пределом последовательности , если для любого все члены последовательности , кроме, быть может, конечного их числа, лежат в -окрестности точки , т.е. найдется такое натуральное число , что при будет выполнено неравенство .

Последовательность может иметь только один предел. Если последовательность имеет предел, то такую последовательность называют сходящейся; последовательность, не имеющую предела, называют расходящейся.

Если последовательность имеет пределом число , то пишут . В этом случае говорят, что последовательность сходится к числу .

Для вычисления пределов последовательностей используются следующие утверждения:

1. Последовательность сходится к числу 0: .

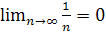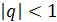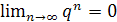2. Последовательность , где , сходится к числу 0: , если .

3. ;

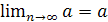4. Теоремы об арифметических операциях над пределами:

Если , а , то:

а) ;

б) ;

в) если , то .

Упражнения с решениями

Пример. Докажите, что .

Доказательство. Пусть – произвольное малое число. Выберем целое положительное число так, чтобы . Тогда, если номер , то и, следовательно, . Таким образом,

Аналогично для любого

.

Задания к практической работе

Задание 1. Докажите, что:

1. ;

2. .

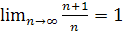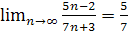Задание 2. Имеют ли предел последовательности:

1. ;

2. .

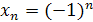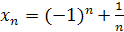Контрольные вопросы

1. Дайте определение понятию предела числовой последовательности.

2. Какая последовательность называется сходящейся?

3. Какая последовательность называется расходящейся?

4. Назовите достаточный признак сходимости последовательности.

Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1

Практическая работа №31

Тема: Суммирование последовательностей, бесконечно убывающая геометрическая прогрессия и ее сумма

Цель: формирование навыков нахождения сумм бесконечно убывающей прогрессии, пределов числовых последовательностей

Вид работы: индивидуальный

Время выполнения: 6 часов

Теоретический материал

Среди геометрических прогрессий особый интерес представляют так называемые бесконечно убывающие геометрические прогрессии.

Начнем с примера. Рассмотрим квадраты, изображенные на рисунке 1. Сторона первого квадрата равна 1, сторона второго равна , сторона третьего - и т.д.

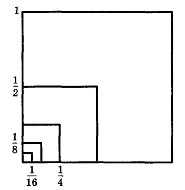
Рис. 1 Квадраты с различными длинами сторон

Таким образом стороны квадрата образуют геометрическую прогрессию со знаменателем :

(1)

Площади этих квадратов образуют геометрическую прогрессию со зна­менателем :

(2)

Из рисунка 1 видно, что стороны квадратов и их площади с возрастанием номера п становятся все меньше, приближаясь к нулю. Поэтому каждая из прогрессий (1) и (2) называется бесконечно убывающей.

Рассмотрим теперь геометрическую прогрессию

Знаменатель этой прогрессии , а ее члены и т. д.

С возрастанием номера п члены этой прогрессии приближаются к нулю. Эту прогрессию также называют бесконечно убывающей. Отметим, что модуль ее знаменателя меньше единицы: .

Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.

Сумма бесконечно убывающей прогрессии есть предел последовательности

Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле

(3)