Упражнения с решениями

Пример 1. Решить уравнение .

Решение. Умножив обе части уравнения на общий знаменатель всех трех дробей, т.е. на , получим , откуда .

Проверка. 1) При знаменатели двух дробей уравнения равны нулю. Поэтому не является корнем данного уравнения.

2. При 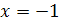левая часть уравнения равна , правая часть равна .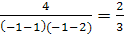

Таким образом, корнем уравнения является , а корень - корнем данного уравнения не является, его называют посторонним корнем.

Пример 2. Решить уравнение .

Решение. Преобразуем данное уравнение так:

,

Откуда , т.е. , следовательно, .

Пример 3. Решить неравенство .

Решение. Так как при всех действительных значениях , то, умножая неравенство на , получаем неравенство , равносильное данному. Решая это неравенство, получаем , , откуда .

Пример 4. Решить неравенство .

Решение.

.

Решая последнее неравенство методом интервалов, получаем .

Пример 5. Решить неравенство .

Решение.

.

Решая последнее неравенство методом интервалов, получаем

.

Задания к практической работе

Задание 1. Равносильны ли следующие уравнения:

1. и ;

2. и ;

3. и ;

4. и ;

5. и ;

6. и ;

7. и ;

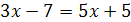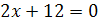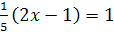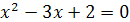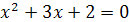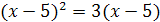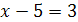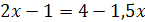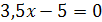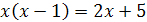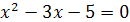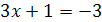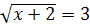8. и .

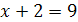Задание 2. Решите уравнения:

1. ;

2. ;

3. ;

4. .

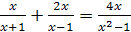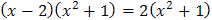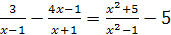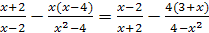Задание 3. Решите неравенства:

1. ;

2. ;

3. ;

4. .

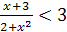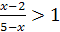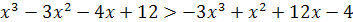Контрольные вопросы

1. Какие уравнения называются равносильными? Приведите примеры.

2. Какое уравнение называется следствием другого? Приведите примеры.

3. Какие методы преобразования уравнений вы знаете?

4. Какие неравенства называются равносильными? Приведите примеры.

Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1

Практическая работа №25

Тема: Рациональные уравнения, приемы их решения

Цель: формирование навыков решения рациональных уравнений, используя различные приемы

Вид работы: индивидуальный

Время выполнения: 4 часа

Теоретические сведения

Уравнение называется рациональным, если и – рациональные выражения.

Чтобы решить рациональное уравнение, нужно:

1. найти общий знаменатель всех имеющихся дробей;

2. заменить данное уравнение целым, умножив обе его части на общий знаменатель;

3. решить полученное целое уравнение;

4. исключить из его корней те, которые обращают в нуль общий знаменатель.

Пример 1. Решить уравнение .

Решение. Общий знаменатель имеющихся дробей является . Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем:

;

;

.

Из уравнения находим . Осталось проверить, обращают ли найденные корни в нуль выражение , т.е. проверить выполнение условия . Замечаем, что 2 не удовлетворяет этому условию, а 4 удовлетворяет. Значит, - единственный корень уравнения.

Решение уравнений методом разложения его левой части на множители.

Суть этого метода состоит в том, что нужно решить уравнение , где – многочлен степени . Предположим, что нам удалось разложить многочлен на множители: , где – многочлены более низкой степени, чем . Тогда уравнение примет вид . Если – корень уравнения , то , а потому хотя бы одно из чисел равно нулю. Значит , - корень хотя бы одного из уравнений

.

Итак, если , где – многочлены, то вместо уравнения нужно решить совокупность уравнений . Все найденные корни этих уравнений, и только они, будут корнями уравнения .

Пример 2. Решить уравнение .

Решение. Разложим на множители левую часть уравнения. Имеем , откуда . Значит, либо , либо . Из первого уравнения находим , второе уравнение корней не имеет. Таким образом, корень уравнения -2.

Решение уравнений методом введения новой переменной

Суть этого метода поясним на примере.

Пример 3. Решить уравнение .

Решение. Положив , получим уравнение , откуда находим . Теперь задача сводится к решению совокупности уравнений

.

Первое квадратное уравнение не имеет действительных корней, так как его дискриминант отрицателен.

Из второго квадратного уравнения находим . Это действительные корни заданного уравнения.

Биквадратные уравнения

Биквадратным называется уравнение вида , где . Биквадратное уравнение решается методом введения новой переменной: положив , придем к квадратному уравнению .

Пример 4. Решить уравнение .

Решение. Положив , получим квадратное уравнение , откуда находим . Теперь задача сводится к решению уравнений . Первое уравнение не имеет действительных корней, из второго находим , которые являются корнями заданного биквадратного уравнения.

Решение задач с помощью составления уравнений

С помощью уравнений решаются многочисленные задачи, к которым приводят самые разнообразные вопросы физики, механики, экономики и многих других прикладных наук. Прежде всего напомним общий порядок решения задач с помощью уравнений.

1. Вводят переменные, т.е. буквами 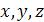обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.

2. С помощью введенных переменных и данных в задаче чисел и их соотношений составляют уравнение.

3. Решают составленное уравнение и из полученных решений отбирают те, которые подходят по смыслу задачи.

4. Если буквами обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.