Упражнения с решениями

Пример 1. Построить график функции

Решение. Область определения функции – вся числовая прямая. Множество значений .

Функция нечетная, периодическая. Период данной функции найдем из равенства . Следовательно, сначала достаточно построить часть графика на отрезке .

Найдем точки пересечения графика с осью . Если , то , откуда , где , т.е. на данном полупериоде кривая пересекает ось в двух точках и .

Максимум функции равен 1 при , т.е. при .

По этим данным построим график функции . Сначала график строим для положительного полупериода (рис. 30), затем на отрезке, соответствующем отрицательному полупериоду , и, наконец, на всей области определения (штриховая линия).

Рис. 30

Пример 2. Построить график функции: 1) .

Решение. Мы знаем, как построить график функции (на рис. 31 он изображен штриховой линией). Растягивая график функции вдоль оси абсцисс в 2 раза, получим график функции .

Затем полученный график растягиваем еще раз, но теперь по оси ординат в 3 раза, получим график функции .

Рис. 31

Пример 3. Построить график функции:

Решение. .

а) область определения – – любое число, кроме , где , так как ;

б) область значений – вся числовая прямая, т.е. ;

в) функция не является ограниченной;

г) функция не принимает экстремальных значений;

д) функция периодическая, главный период , так как ;

е) функция не является монотонной на всей области определения, но функция возрастает на каждом из промежутков, , где ;

точки пересечения с осями координат – точки , где , так как при , т.е. .

Учитывая периодичность, построим график функции .

Рис. 32

Пример 4. Построить график функции: , используя формулу приведения.

Решение. По формуле приведения . Поэтому график функции можно получить из графика функции с помощью параллельного переноса влево на (рис. 33) и симметрией относительно оси абсцисс. График функции изображен на рисунке 34.

Рис. 33

Рис. 34

Задания к практическому занятию

Задание 1. Постройте график функции:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

Задание 2. Постройте график функции:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

Задание 3. Постройте график функции:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

Задание 4. Постройте график функции:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

Контрольные вопросы

1. Перечислите основные свойства синуса.

2. Перечислите основные свойства косинуса.

3. Перечислите основные свойства тангенса.

4. Перечислите основные свойства котангенса.

Рекомендуемая литература: 1.1, 1.3, 1.4

Практическое занятие №22

Тема: Обратные тригонометрические функции: определения, свойства, графики

Цель: формирование навыков построения графиков обратных тригонометрических функций, определения их области определения и множества значений

Вид работы: индивидуальный

Время выполнения: 2 часов

Теоретический материал

Функция

Перечислим основные свойства функции .

1. Область определения – отрезок .

2. Множество значений – отрезок .

3. Функция возрастает.

4. Функция является нечетной, так как .

График функции симметричен графику функции , относительно прямой (рис. 35).

Рис. 35

Функция

Перечислим основные свойства функции .

1. Область определения – отрезок .

2. Множество значений – отрезок .

3. Функция убывает.

График функции симметричен графику функции , относительно прямой (рис. 36).

Рис. 36

Функция

Перечислим основные свойства функции .

1. Область определения – множество всех действительных чисел.

2. Множество значений – интервал .

3. Функция возрастает.

4. Функция является нечетной: .

График функции получается из графика функции , , симметрией относительно прямой (рис. 37).

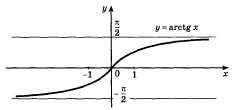
Рис. 37

Упражнения с решениями

Пример 1. Найти область определения функции

.

Решение. Так как функция определена при , то функция определена для тех значений , для которых выполняются неравенства . Отсюда , .

Пример 2. Решить уравнение .

Решение. Так как , то по определению арккосинуса числа данное уравнение равносильно уравнению , откуда , .

Задания к практическому занятию

Задание 1. Найти область определения функции:

1. ;

2. ;

3. ;

4. .

Задание 2. Доказать, что график функции симметричен относительно точки .

Задание 3. Решить уравнение:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

Контрольные вопросы

1. Дайте определение функции .

2. Дайте определение функции .

3. Дайте определение функции .

4. Дайте определение функции .

5. Перечислите свойства обратных тригонометрических функций.

Рекомендуемая литература: 1.1, 1.3, 1.4

Практическое занятие №23

Тема: Основные преобразования графиков

Цель: формирование навыков построения графиков функций и выполнения их основных преобразований

Вид работы: индивидуальный

Время выполнения: 2 часа

Теоретический материал

Если известен график функции , то с помощью некоторых преобразований плоскости (параллельного переноса, осевой и центральной симметрии и т.п.) можно построить графики более сложных функций.

1. График функции получается сжатием графика в раз к оси при или растяжением в раз от этой оси при (рис.38).

Рис.38

2. График функции получается параллельным переносом графика в отрицательном направлении оси на при и в положительном направлении на при (рис.39).

Рис. 39

3. График функции получается растяжением графика вдоль оси в раз при и сжатием вдоль этой оси в раз при (рис.40).

Рис. 40

4. График функции получается параллельным переносом графика в положительном направлении оси на при и в отрицательном направлении этой оси на при (рис.41).

Рис. 41

5. График функции получается симметричным отображением графика относительно оси (рис.42).

6. График функции получается симметричным отображением графика относительно оси (рис.43).

7. График функции получается из графика функции следующим образом: часть графика , лежащая над осью , сохраняется, часть его, лежащая под осью , отображается симметрично относительно оси (рис.44).

8. График функции получается из графика функции следующим образом: при график сохраняется, а при полученная часть графика отображается симметрично относительно оси (рис.45).

Рис. 42 Рис. 43 Рис. 44 Рис. 45