
- •Министерство образования и науки российской федерации
- •230115 Программирование в компьютерных системах
- •230401 Информационные системы (по отраслям)
- •Пояснительная записка
- •Общие требования к выполнению практических занятий:
- •Критерии оценки практических работ
- •Практическая работа №9
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №10
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №11
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №12
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №13
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №14
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №16
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Список литературы
- •1. Основная:
- •2. Дополнительная:
Теоретические сведения
Функция ![]() на отрезке
на отрезке ![]() имеет обратную функцию, которая
называется арксинусом
и обозначается
имеет обратную функцию, которая
называется арксинусом
и обозначается ![]() .
.
![]() ,
где
,
где ![]() .
.
![]() .
.
Функция ![]() на отрезке
на отрезке ![]() имеет обратную функцию, которая
называется арккосинусом
и обозначается
имеет обратную функцию, которая
называется арккосинусом
и обозначается ![]() .
.
![]() ,
где
.
,
где
.
![]() .
.
Функция ![]() на промежутке
на промежутке ![]() имеет обратную функцию, которая
называется арктангенсом
и обозначается
имеет обратную функцию, которая
называется арктангенсом
и обозначается ![]() .
.
![]() ,
где
,
где ![]() .
.
![]() .
.
Функция ![]() на
промежутке
на
промежутке ![]() имеет обратную функцию, которая
называется арккотангенсом
и обозначается
имеет обратную функцию, которая
называется арккотангенсом
и обозначается ![]() .
.
![]() ,
где
.
,
где
.
![]() .
.
Упражнения с решениями
Пример. Проверить справедливы ли равенства:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
Решение:
1)
,
так как ![]() и
и ![]() .
.
, так как
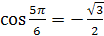 и
и  .
., так как
 и
и  .
.
Задания к практическому занятию
Задание 1. Проверьте, справедливы ли равенства:
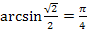 ;
; ;
; ;
; ;
; ;
; ;
; ;
;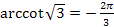 .
.
Задание 2. Вычислите:
 ;
;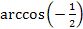 ;
; ;
; ;
; .
.
Задание 3. Докажите справедливость неравенств:
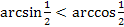 ;
; ;
; ;
;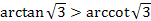 .
.
Задание 4. Вычислите:
 ;
; ;
; ;
;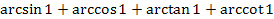 ;
; ;
;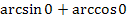 ;
;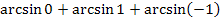 ;
; .
.
Контрольные вопросы
Что называется арксинусом?
Что называется арккосинусом?
Что называется арктангенсом?
Что называется арккотангенсом?
Как вычислить арксинус, арккосинус, арктангенс и арккотангенс от отрицательного значения?
Рекомендуемая литература: 1.1, 1.4
Практическая работа №15
Тема: Простейшие тригонометрические уравнения
Цель: формирование навыков решения тригонометрических уравнений
Вид работы: индивидуальный
Время выполнения: 2 часа
Теоретические сведения
Простейшими
тригонометрическими уравнениям
называют уравнения ![]() ,
где
,
где ![]() - данное число.
- данное число.
Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента (дуг или углов), при которых данная тригонометрическая функция принимает заданное значение .
Формула для корней
уравнения ![]() ,
где
,
где ![]() ,
имеет вид:
,
имеет вид:
![]() . (1)
. (1)
Частные случаи:
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() . (4)
. (4)
Формула для корней
уравнения ![]() ,
где
,
где ![]() ,
имеет вид:
,
имеет вид:
![]() . (5)
. (5)
Формула для корней
уравнения ![]() ,
где
,
имеет вид:
,
где
,
имеет вид:
![]() . (6)
. (6)
Частные случаи:
![]() ; (7)
; (7)
![]() ; (8)
; (8)
![]() . (9)
. (9)
Формула для корней
уравнения ![]() ,
где
,
имеет вид:
,
где
,
имеет вид:
![]() . (10)
. (10)
Формула для корней
уравнения ![]() ,
имеет вид:
,
имеет вид:
![]() . (11)
. (11)
Частные случаи:
![]() ; (12)
; (12)
![]() ; (13)
; (13)
![]() . (14)
. (14)
Формула для корней
уравнения ![]() ,
где
,
где ![]() ,
имеет вид:
,
имеет вид:
![]() . (15)
. (15)
Упражнения с решениями
Пример 1. Решить
уравнения: 1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]()
Решение.
1) ![]() ,
отсюда следует, что множество корней
данного уравнения имеет вид
,
отсюда следует, что множество корней
данного уравнения имеет вид ![]() .
.
Так как
 и
и 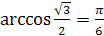 ,
то
,
то 
 .
Тогда множество корней уравнения имеет
вид
.
Тогда множество корней уравнения имеет
вид 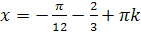 .
.
Пример 2. Решить
уравнение ![]() .
.
Решение.
Заменяя ![]() на
на ![]() ,
получаем
,
получаем ![]() или
или ![]() .
.
Обозначая ![]() ,
получаем
,
получаем ![]() ,
откуда
,
откуда ![]() ,
,
![]() .
.
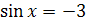 - уравнение не имеет корней, так как
- уравнение не имеет корней, так как
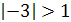 ;
;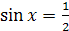 ,
,
 .
.
Таким образом,
![]() .
.
Пример 3.
Решить уравнение ![]() .
.
Решение.
Используя формулы ![]() ,
,
![]() и записывая правую часть уравнения в
виде
и записывая правую часть уравнения в
виде ![]() ,
получаем
,
получаем ![]() ,
,
![]() .
.
Поделив это
уравнение на ![]() ,
получим равносильное уравнение
,
получим равносильное уравнение ![]() .
Обозначая
.
Обозначая ![]() ,
получим уравнение
,
получим уравнение ![]() ,
откуда
,
откуда ![]() ,
,
![]() .
.
 ;
;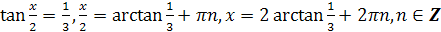 .
.
