
- •Министерство образования и науки российской федерации
- •230115 Программирование в компьютерных системах
- •230401 Информационные системы (по отраслям)
- •Пояснительная записка
- •Общие требования к выполнению практических занятий:
- •Критерии оценки практических работ
- •Практическая работа №9
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №10
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №11
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №12
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №13
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №14
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Практическая работа №16
- •Теоретические сведения
- •Упражнения с решениями
- •Задания к практическому занятию
- •Контрольные вопросы
- •Список литературы
- •1. Основная:
- •2. Дополнительная:
Упражнения с решениями
Пример 1.
Определить знак произведения ![]() .
.
Решение.
![]() ,
так как угол
,
так как угол ![]() является
углом первой четверти, а синус в первой
четверти положителен.
является
углом первой четверти, а синус в первой
четверти положителен.
![]() ,
так как угол
,
так как угол ![]() является
углом третьей четверти, а косинус в
этой четверти отрицателен.
является
углом третьей четверти, а косинус в
этой четверти отрицателен.
![]() ,
так как угол
,
так как угол ![]() является
углом первой четверти, а косинус в этой
четверти положителен.
является
углом первой четверти, а косинус в этой
четверти положителен.
![]() ,
так как угол
,
так как угол ![]() является
углом четвертой четверти, а синус в
этой четверти отрицателен.
является
углом четвертой четверти, а синус в
этой четверти отрицателен.
![]() ,
так как угол
является
углом четвертой четверти, а косинус в
этой четверти положителен.
,
так как угол
является
углом четвертой четверти, а косинус в
этой четверти положителен.
![]() ,
так как угол, величина которого 2 радиана,
является углом второй четверти, а синус
в этой четверти положителен.
,
так как угол, величина которого 2 радиана,
является углом второй четверти, а синус
в этой четверти положителен.
Следовательно, произведение положительно.
Пример 2. Сравнить значения выражений:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Решение.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
![]() .
.
Пример 3.
Доказать тождество ![]()
Доказательство. В левой части тождества произведем указанные действия и приведем подобные члены, получим:
![]() .
.
Левую часть равенства преобразуем так:
![]() Следовательно,
Следовательно,
![]() .
Тождество доказано.
.
Тождество доказано.
Задания к практическому занятию
Задание 1. Найти радианную меру угла, выраженного в градусах:
 ;
;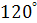 ;
; ;
;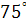 ;
; ;
;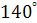 .
.
Задание 2. Найти градусную меру угла, выраженного в радианах:
 ;
; ;
;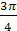 ;
;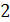 ;
;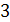 ;
; ,36.
,36.
Задание 3. Определите знак произведения.
 ;
;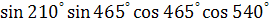 ;
;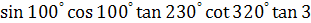 ;
;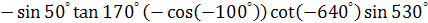 .
.
Задание 4. Упростите выражение:
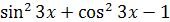 ;
;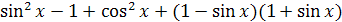 ;
;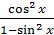 ;
;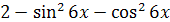 .
.
Задание 5. Вычислите значение , если:
 ;
;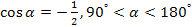 ;
;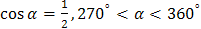 ;
; ;
;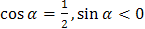 ;
;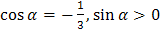 .
.
Задание 6. Докажите тождество:
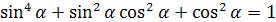 ;
; ;
;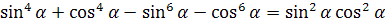 .
.
Задание 7. Найдите значение выражения:
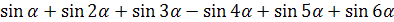 ,
при
,
при  ;
;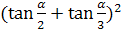 ,
при
,
при  ;
; .
.
Контрольные вопросы
Назовите единицы измерения величины угла.
Что принимается за ; за 1 радиан?
Что называется синусом угла ?
Что называется косинусом угла ?
Дайте определения тангенса и котангенса числа ?
Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1
Практическая работа №11
Тема: Основные тригонометрические тождества. Формулы приведения
Цель: формирование навыков использования формул приведения при доказательстве тригонометрических тождеств
Вид работы: индивидуальный
Время выполнения: 2 часа
Теоретические сведения
Равенство, справедливое при всех допустимых значениях входящих в него букв (т.е. таких, при которых его левая и правая части имеют смысл), называют тождеством, а задачи на доказательство таких равенств называют задачами на доказательство тождеств.
Существуют следующие способы доказательства тождеств: преобразование левой части к правой; преобразование правой части к левой; установление того, что разность между левой и правой частями равна нулю. Иногда удобно доказательство тождества провести преобразованием его левой и правой частей к одному и тому же выражению.
 . (1)
. (1). (2)
. (3)
. (4)
. (5)
 . (6)
. (6). (7)
Из формул (4) и (5) следует, что
![]() (8)
(8)
Из формулы (8) следует, что
![]() (9)
(9)
![]() (10)
(10)
Разделив обе части равенства (1) на
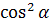 ,
получим:
,
получим:
![]() (11)
(11)
Разделив обе части равенства (1) на
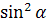 ,
получим:
,
получим:
![]() (12)
(12)
Формулами
приведения
называются соотношения, с помощью
которых значения тригонометрических
функций аргументов ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
выражаются через значения
,
выражаются через значения ![]() .
.
Все формулы приведения можно свести в следующую таблицу:
Таблица 3
Функция |
Аргумент |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для облегчения запоминания приведенных формул нужно использовать следующие правила:
при переходе от функций углов , к функциям угла название функции изменяют: синус на косинус, тангенс на котангенс и наоборот;
при переходе от функций углов , к функциям угла название функции сохраняют;
считая
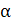 острым углом (т.е.
острым углом (т.е. 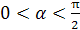 ),
перед функцией угла
ставят такой знак, какой имеет приводимая
функция углов
),
перед функцией угла
ставят такой знак, какой имеет приводимая
функция углов  ,
,
 ,
,
 .
.
Исходя из известных значений тригонометрических функций некоторых углов, соответствия между градусной и радианной мерой величины угла и формул приведения, можно составить таблицу значений тригонометрических функций для наиболее часто встречающихся значений аргумента:
Таблица 4
Функция |
Аргумент |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не сущ. |
|
|
|
|
|
|
|
Не сущ. |
|
|
|
|
|
Не сущ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не сущ. |
