Задания к практическому занятию

Задание 1. Упростите выражение:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

Задание 2. Разложите многочлен на множители:

1. ;

2. ;

3. ;

4. 

5. 

6. −1.

Задание 3. Разложите на множители квадратный трехчлен:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

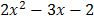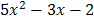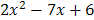Задание 4.Упростите выражение:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

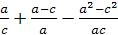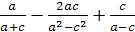Задание 5. Сократите дробь

1. ;

2. ;

3. ;

4. .

Задание 6. Найдите область определения дроби:

1. ;

2. ;

3. ;

4. .

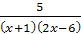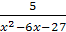Задание 7. Извлечь корень из произведения .

Задание 8. Вынести множитель из-под знака корня .

Задание 9. Упростить

1. ;

2. ;

3. ;

4. 

5. ;

6. .

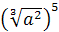Задание 10. Упростите выражение и найдите его значение:

1. , при ;

2. , при ;

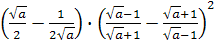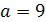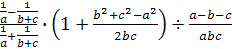3. , при .

Задание 11. Упростите выражение:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

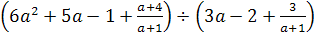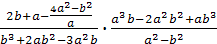Задание 12. Докажите тождество:

1. ;

2. ;

3. ;

4. .

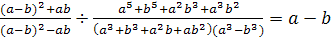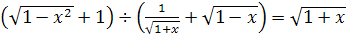Контрольные вопросы

1. Что называется алгебраическим выражением?

2. Какие виды алгебраических выражений существуют?

3. Что называется областью определения алгебраического выражения?

4. Дайте определение одночлена и многочлена?

5. Назовите основные способы разложения многочлена на множители.

6. Назовите основные приемы преобразований рациональных выражений.

Рекомендуемая литература: 1.1, 1.3, 1.4

Практическая работа №10

Тема: Радианная мера угла. Вращательное движение, синус, косинус, тангенс, котангенс

Цель: формирование навыков вычислений синусов, косинусов, тангенсов и котангенсов углов

Вид работы: индивидуальный

Время выполнения: 2 часа

Теоретические сведения

Угол в 1 радиан есть центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности (рис. 1)

Рис. 1 Центральный угол

Если начальный радиус совершит один полный оборот, то получится угол, равный или радианам.

Радианная мера равна .

Если угол содержит , то его радианная мера равна

(1)

Из равенства (1) следует, что угол, равный радианам, содержит

градусов (2)

Длина дуги в радиан определяется по формуле:

( – радиус окружности) (3)

Длина дуги в определяется по формуле

(4)

Из формулы следует:

; ; ; и т.д.

Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом равным 1. На единичной окружности отметим точку . При повороте начального радиуса около центра на угол радиан точка перейдет в некоторую точку . Обозначим координаты этой точки и . (Заметим, что поворот можно осуществить как в положительном, так и отрицательном направлении.)

Синусом угла называется отношение ординаты точки к радиусу. Таким образом .

Косинусом угла называется отношение абсциссы точки к радиусу. Таким образом .

Каждому углу соответствует единственная точка и, следовательно, единственное значение синуса и косинуса этого числа.

Координаты любой точки единичной окружности удовлетворяют уравнению: . Отсюда , где .

Из этой формулы следует, что: ; .

В практических вычислениях часто используются значения синуса и косинуса, приведенные в таблице 1:

Таблица 1

Знаки значений функций синуса и косинуса. Знаки и определяются знаками ординаты и абсциссы соот­ветствующей точки единичной окружности. Если ( в первой координатной четверти), то числу соответствует точка окружности , координаты которой и . Следовательно, на числовом промежутке , (рис. 2).

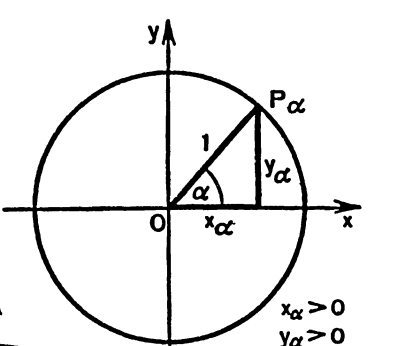
Рис. 2

Если ( во второй координатной четверти), то, рассуждая аналогично, получаем , (рис. 3)

Если ( в третьей координатной четверти), то имеем , (рис. 4).

Рис. 3 Рис.4

Если ( в четвертой координатной четверти), то , (рис. 5).

Рис. 5

Схематически знаки изображены на рисунке 6, а, а на рисунке 6, б.

Рис. 6

Тангенсом числа называется отношение ординаты точки к ее абсциссе (рис. 7). Таким образом, .

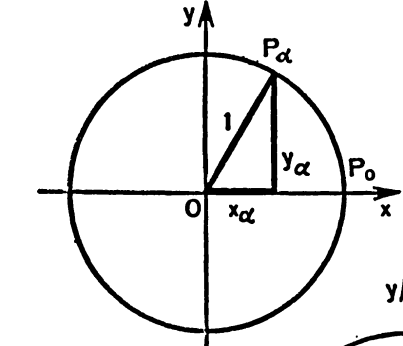
Рис. 7

Котангенсом числа называется отношение абсциссы точки к ее ординате (рис. 8). Таким образом, .

Значения тангенса и котангенса для чисел

Знаки значений функций тангенса и котангенса. Знаки значений легко найти из формул и .

Аналогично находим остальные значения. Заметим, что для некоторых чисел и не существуют. Например, (не имеет смысла).

Приведем таблицу этих значений:

Таблица 2

					Не существует		Не существует
	Не существует					Не существует		Не существует

Знаки значений функций тангенса и котангенса можно определить по знакам значений синуса и косинуса. Так как в I и III четвертях знаки значений синуса и косинуса одинаковые, а именно в I четверти и , а в III четверти и , то в этих четвертях и .

Так как во II и IV четвертях знаки значений синуса и косинуса разные, а именно во II четверти , , а в IV четверти , , то в этих четвертях и . Заметим, что знаки значений тангенса и котангенса можно лег­ко определить по знаку ординаты и абсциссы.

Секансом числа , называется величина, обратная , т. е. .

Косекансом числа , называется величина, обратная , т. е. .