
Государственное общеобразовательное учреждение
Высшее профессиональное образование
Дальневосточный государственный университет путей сообщения
Кафедра «Физика»
Т.К. Толкунова
Изучение затухающих колебаний
на примере физического маятника
Методические указания на выполнение
лабораторной работы
Хабаровск
2007
Цель работы:
1. Определить период колебаний физического маятника.
2. Определить коэффициент затухания физического маятника.
Приборы и принадлежности: Кронштейн с линейкой, металлический стержень, набор грузов, секундомер.
1. Теоретическая часть
1.1. Гармонические колебания
Колебательным движением или просто колебанием называется изменение состояния, характеризуемого повторяемостью во времени значений физических величин, характеризующих это состояние.
К
Т
X, м
+А
-А
0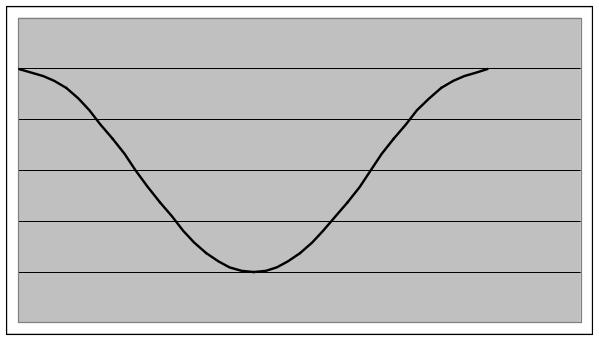




t, c![]()
Рис .1.1. График зависимости смещения от времении
Уравнения (1.1) называются уравнениями
собственных свободных колебаний, где
Х - смещение точки от положения
равновесия; А – амплитуда колебаний
– величина, равная максимальному
смещению от положения равновесия;
![]() - фаза колебания точки, стоит под знаком
косинуса и определяет долю, которую
смещение составляет от максимального;
- фаза колебания точки, стоит под знаком
косинуса и определяет долю, которую
смещение составляет от максимального;
![]() - начальная фаза колебаний точки; ω
– циклическая или угловая частота
колебаний - величина, определяемая
числом полных колебаний, совершаемых
за 2π секунд.
- начальная фаза колебаний точки; ω
– циклическая или угловая частота
колебаний - величина, определяемая
числом полных колебаний, совершаемых
за 2π секунд.
![]() , (1.2)
, (1.2)
г
Рис. 1.1. График
зависимости смещения от времени![]() - период колебаний – наименьший промежуток
времени, по истечении которого повторяются
значения всех физических величин,
характеризующих колебания или время,
в течение которого совершается полное
колебательное движение. На рис. 1.1
представлен график гармонических
колебаний, зависимости смещения Х
от времени t, начальная
фаза которого
- период колебаний – наименьший промежуток
времени, по истечении которого повторяются
значения всех физических величин,
характеризующих колебания или время,
в течение которого совершается полное
колебательное движение. На рис. 1.1
представлен график гармонических
колебаний, зависимости смещения Х
от времени t, начальная
фаза которого
![]() ,
описываемого уравнением
,
описываемого уравнением
![]() . (1.3)
. (1.3)
При гармоническом колебательном движении смещение точки меняется со временем по закону (1.3). Дифференцируя это выражение по времени t, находим скорость движения точки в любой момент времени t
![]() . (1.4)
. (1.4)
Дифференцируя уравнение (1.4) еще раз по времени t, найдем зависимость ускорения точки в любой момент времени
![]() . (1.5)
. (1.5)
И
X, м
a
υ
+A
-a
-υ
-A
a(t)
υ(t)
x(t)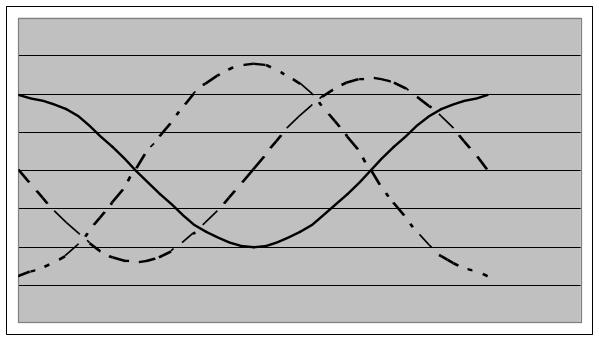




![]() .
Максимальное значение скорости равно
.
Максимальное значение скорости равно
![]() ,
а максимальное значение ускорения
,
а максимальное значение ускорения
![]() .
Колебания скорости опережают колебания
смещения по фазе на
.
Колебания скорости опережают колебания
смещения по фазе на
![]() ,
а колебания ускорения опережают колебания
смещения по фазе на π рис. 1.2.
,
а колебания ускорения опережают колебания
смещения по фазе на π рис. 1.2.
Рис. 1.2. График гармонических колебаний
1.2. Затухающие колебания
В условиях, когда на тело действует только одна квазиупругая сила, тело будет совершать свободные незатухающие гармонические колебания с постоянной амплитудой А=const. В реальных условиях на тело действует со стороны окружающей среды сила трения, препятствующая его движению. На преодоление сопротивления среды, трение в опорах, создание волн и .т.п. будет затрачиваться энергия. Вследствие этого механическая энергия колеблющегося тела будет непрерывно уменьшаться. Полная энергия Е материальной точки массой m, совершающая гармонические колебания с частотой ω и амплитудой А.
![]() . (1.6)
. (1.6)
Таким образом, полная энергия гармонически
колеблющейся точки есть величина
постоянная и пропорциональная квадрату
амплитуды колебаний
![]() .
.
С уменьшением энергии в реальных системах будет уменьшаться амплитуда, и колебание станет звтухающим.
Полная сила F, действующая
на колеблющуюся точку, будет суммой
квазиупругой силы
![]() и силы трения
и силы трения
![]() .
При малых скоростях движения сопротивление
обычно пропорционально первой степени
скорости и направленной противоположно
ей:
.
При малых скоростях движения сопротивление
обычно пропорционально первой степени
скорости и направленной противоположно
ей:
![]() , (1.7)
, (1.7)
где r – коэффициент
трения, зависящий от свойств среды,
формы и размеров движущегося тела.
Запишем полное выражения силы
![]() ,
подставим это выражение во второй закон
Ньютона, получим
,
подставим это выражение во второй закон
Ньютона, получим
![]() ,
или
,
или
![]() (1.8)
(1.8)
Уравнение (1.8) есть дифференциальное уравнение затухающих колебаний материальной точки массой m. Решение дифференциального уравнения (1.8) имеет вид
![]() ,(1.9)
,(1.9)
где
![]() ,
,
,
,
![]() ,
,
![]() - постоянные величины. Вычисляя первую
и вторую производные от выражения (1.9)
и подставляя найденные значения Х,
- постоянные величины. Вычисляя первую
и вторую производные от выражения (1.9)
и подставляя найденные значения Х,
![]() и
и
![]() в (1.8), получим
в (1.8), получим
![]() .
.
Множитель
![]() можно сократить, так как
– постоянная, а
можно сократить, так как
– постоянная, а
![]() при определенном значении t
не обращается в нуль. Оставшееся выражение
будет равно нулю при любых значениях
t, если порознь будут
равны нулю коэффициенты при
при определенном значении t
не обращается в нуль. Оставшееся выражение
будет равно нулю при любых значениях
t, если порознь будут
равны нулю коэффициенты при
![]() и
и
![]() .
Действительно, в некоторый момент
времени t функция
обратится в нуль. При этом
будет равен
.
Действительно, в некоторый момент
времени t функция
обратится в нуль. При этом
будет равен
![]() .
Следовательно, это равенство будет
удовлетворяться, если коэффициент при
равен нулю. Аналогично можно доказать
равенство нулю множителя при
.
Таким образом получим два уравнения
.
Следовательно, это равенство будет
удовлетворяться, если коэффициент при
равен нулю. Аналогично можно доказать
равенство нулю множителя при
.
Таким образом получим два уравнения
![]()
Решая эти уравнения, находим
![]() , (1.10)
, (1.10)
![]() .
(1.11)
.
(1.11)
Выражение (1.9), в котором значения β и ω определены из (1.10) и (1.11), является общим решением уравнения затухающих колебаний (1.8). Амплитуда колебания
![]() . (1.12)
. (1.12)
Является убывающей функцией. На рис 1.3. представлен график зависимости смещения от времени t для затухающих колебаний, описываемых уравнением (1.9) (сплошная линия). Пунктиром изображена зависимость (1.12) амплитуды от времени t.
Чем больше коэффициент трения r,
тем больше коэффициент затухания β,
тем быстрее амплитуда затухающих
колебаний убывает со временем. При
полном отсутствии трения происходит
гармоническое колебание с циклической
частотой
![]() .
При наличии
.
При наличии
Р
t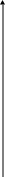

трения не только убывает со временем амплитуда колебания, но и уменьшается угловая частота колебаний:
![]() . (1.13)
. (1.13)
где
![]() - циклическая частота собственных
колебаний точки при отсутствии трения.
Соответственно период затухающих
колебаний равен
- циклическая частота собственных
колебаний точки при отсутствии трения.
Соответственно период затухающих
колебаний равен
![]() . (1.14)
. (1.14)
С увеличением трения период возрастает,
и при
увеличением трения период возрастает,
и при
![]() период становится бесконечным:
период становится бесконечным:
![]() .
.
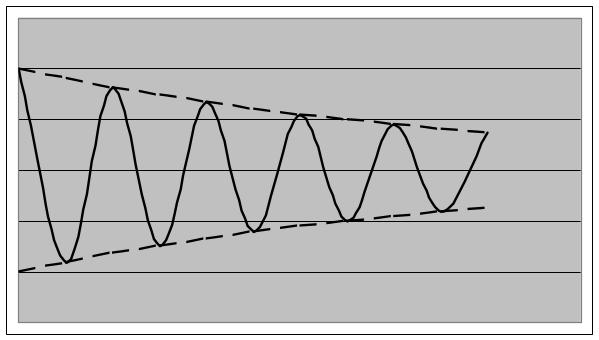
При дальнейшем увеличении период становится мнимым, а движение точки апериодическим (рис. 1.4).
Сопоставим при
![]() значения амплитуд в моменты времени,
отличающиеся друг от друга на один
период:
и
значения амплитуд в моменты времени,
отличающиеся друг от друга на один
период:
и
![]() ,
и разделим первое на второе. Получаем
,
и разделим первое на второе. Получаем
![]() , (1.15)
, (1.15)
То есть амплитуда затухающих колебаний за каждый период убывает в одно и то же число раз. Логарифм отношения двух соседних амплитуд носит название логарифмического декремента затухания
![]() . (1.16)
. (1.16)
Время τ, в течении которого амплитуда
уменьшается в e раз,
называется временем релаксации. За
время релаксации система совершает
![]() колебаний
колебаний
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
следовательно коэффициент затухания
β есть физическая величина, обратная
времени релаксации
,
следовательно коэффициент затухания
β есть физическая величина, обратная
времени релаксации
![]() .
Логарифмический декремент затухания
обратно пропорционален по величине
числу колебаний N,
совершаемых за время релаксации.
.
Логарифмический декремент затухания
обратно пропорционален по величине
числу колебаний N,
совершаемых за время релаксации.
Характеристикой колебательной системы служит величина, называемая добротностью колебательной системы, которая при малых значениях логарифмического декремента равна
![]() .
.
Так как затухания невелики (![]() ),
то принято равным Т0.
Величину добротности можно представить
через энергетические характеристики
колеблющейся системы
),
то принято равным Т0.
Величину добротности можно представить
через энергетические характеристики
колеблющейся системы
![]() , (1.17)
, (1.17)
где Е – энергия колебаний системы в произвольный момент времени t, ΔЕ – убыль этой энергии за промежуток времени от t до t+T, то есть за один условный период затухающих колебаний.
