9.2Закон збереження енергії в механічних процесах.

Енергія вимірюється тими самими одиницями (Дж).

Повна механічна енергія тіла біля поверхні Землі дорівнює:

 П =  + mgh + 

Повна механічна енергія замкнутої системи тіл, які взаємодіють

силами тяжіння і пружності, залишається незмінною.

 + mgh₁ +   ⁼   + mgh₂ +   - закон збереження енергії в механічних процесах.

 

 Пмакс = К1 + П1 = Кмакс

10. Кінематика обертового руху

Величину, яка дорівнює відношенню зміни швидкості тіла до інтервалу часу, протягом якого ця зміна відбулася, називають середнім прискоренням:

Прискорення – величина векторна; напрям вектора прискорення завжди співпадає з напрямом вектора зміни швидкості.

Миттєве прискорення, тобто прискорення у даний момент часу або прискорення у даній точці траєкторії руху визначається границею, до якої прямує величина при :

У загальному випадку плоского криволінійного руху вектор прискорення зручно представляти у вигляді суми двох проекцій:

Тангенціальне прискорення характеризує зміну швидкості за величиною і напрямлене по дотичній до даної точки траєкторії:

Нормальне, або доцентрове, прискорення характеризує зміну швидкості за напрямом і напрямлене вздовж миттєвого радіуса кривизни R до центра:

Модуль і напрям повного прискорення в даній точці траєкторії відповідно визначається як:

11. Моментом імпульсу матеріальної точки відносно початку координат в класичній механіці є величина, яка дорівнює векторному добутку радіус-вектора цієї частинки на її імпульс.

Відповідно,

L -- кутовий момент

r -- радіус-вектор частинки

p -- імпульс частинки

Якщо фізична система складається з багатьох матеріальних точок, то результуючий момент імпульсу відносно початку координат є сумою (інтегралом) усіх моментів імпульсу складових системи.

Для багатьох практичних задач, які вивчають властивості об'єкта, що обертається навколо певної осі, достатньо проаналізувати скалярне значення момента імпульсу, який є додатним, якщо обертання відбувається проти годинникової стрілки та від'ємним, якщо навпаки.

Відповідно до визначення векторного добутку векторів, скаляр момента імпульсу визначається як:

де θr,p -- кут між r та p, який вимірюється від r до p; такий порядок обходу векторів при визначенні кута є принциповим. Якщо порядок змінити на зворотний, зміниться й знак.

Для тіла сталої маси, яке обертається навколо фіксованої осі, момент імпульсу можна визначити як добуток момента інерції тіла відносно цієї осі на його кутову швидкість:

де I -- момент інерції частинки, ω -- вектор кутової швидкості.

12. Теоре́ма Гю́йгенса — Штейнера, або теорема Штейнера (названа іменами швейцарського математика Якова Штейнера і нідерландського математика, фізика і астронома Хрістіана Гюйгенса): момент інерції тіла   відносно довільної осі дорівнює сумі моменту інерції цього тіла   відносно осі, що проходить через центр маси тіла паралельно до осі, що розглядається і добутку маси тіла   на квадрат відстані   між осями:

.

Момент інерції досягає свого мінімального значення, коли вісь проходить через центр мас.

Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, становить:

Момент інерції

Моментом інерції матеріальної точки відносно осі обертання називається добуток маси цієї точки на квадрат відстані від осі:

Моментом інерції системи (тіла) відносно осі обертання називається фізична величина, яка дорівнює сумі добутків мас n матеріальних точок на квадрати їх відстаней до даної осі:

Головний момент інерції – це момент інерції відносно головної осі, яка проходить через центр мас. Момент інерції тіла залежить відносно якої осі воно обертається і як розподілена маса тіла по об'єму.

Момент інерції:

* однорідного циліндра (диска):

де R – радіус циліндра; m – його маса;

* товстостінного циліндра:

де R1 і R2 – зовнішній і внутрішній радіуси циліндра;

* тонкостінного циліндра:

де R – радіус циліндра;

* суцільної кулі:

де R – радіус кулі;

* однорідного стержня довжиною l, вісь обертання якого проходить перпендикулярно до середини стержня:

13. Моме́нт си́ли — векторна фізична величина, рівна векторному добутку радіус-вектора, проведеного від осі обертання до точки прикладення сили, на вектор цієї сили. Момент сили є мірою зусилля, направленого на обертання тіла.

Момент сили зазвичай позначається латинською літерою і вимірюється в системі СІ в Н м. M₀ = r*F Векторна величина M0, рівна векторному добутку радіуса-вектора r, проведеного з O в точку прикладання сили F, на силу.

Відповідно до рівняння другий закон Ньютона для обертального руху

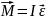. За визначенням кутове прискорення і тоді це рівняння можна переписати таким чином . або Це вираз носить назву основного рівняння динаміки обертального руху і формулюється таким чином: зміна моменту кількості руху твердого тіла, дорівнює імпульсу моменту всіх зовнішніх сил, що діють на це тіло.

14. Закон збереження моменту імпульсу стверджує, що момент кількості руху у замкненій системі зберігається під час еволюції цієї системи з часом. Момент імпульсу замкнутої системи тіл залишається незмінним при будь-яких взаємодіях тіл системи. Закон збереження кількості руху є наслідком ізотропності простору.

15. Кінетична енергія обертального руху - енергія тіла, пов'язана з його обертанням. Основні кінематичні характеристики обертального руху тіла - його кутова швидкість (ω) і кутове прискорення. Основні динамічні характеристики обертального руху - момент імпульсу відносно осі обертання z:

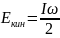
Якщо тіло котиться, то його кінетична енергія складається з кінетичної енергії поступального руху і кінетичної енергії обертового руху. Загальна формула: E = (m * v ^ 2) / 2 + (I * w ^ 2) / 2; I - момент інерції тіла, w-кутова швидкість тіла, m-маса тіла, v-швидкість поступального руху тіла.