Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Международный экономико-гуманитарный университет им. С. Демьянчука

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

08_lb_AD.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

1.39 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Лабораторна робота 2. Кореляційний аналіз

2.1 Мета роботи – для заданої багатовимірної сукупності даних виявити наявність або відсутність кореляційного зв’язку, виявити силу та значимість кореляційного зв’язку.

2.2 Завдання та теоретична частина

2.2.1 Наявні результати спостережень протягом 40 діб за показниками природного водойму:

Х₁ – температура, С
Х₂ – вміст хлоридів, гм^-3,
Х₃ – вміст загального азоту, гм^-3,
Х₄ – хімічне споживання кисню, гм^-3
Х₅ – концентрація синьо-зелених водоростей, 1/см³,
Х₆ – концентрація Е.coli, 1/см³,
Х₇ – вміст фосфатів, гм^-3,
Х₈ – вміст фенолів, мгм^-3
Х₉ – вміст сульфатів, мгм^-3.

Необхідно виявити наявність кореляцій між цими величинами, парні і множні.

2.2.2 Теоретична частина міститься у розділі 3 лекційного курсу. Для виконання роботи необхідно проробити матеріал, виписати розрахункові формули і алгоритми.

2.3 Приклад виконання завдання

2.3.1 Вхідні дані для розрахунків наведено у таблиці 2.1.

2.3.2 Вхідні дані переносимо на робочий аркуш Excel

Таблиця 2.1 – Вхідні дані

№	Х₁	Х₂	Х₃	Х₄	Х₅	Х₆	Х₇	Х₈	Х₉
1	25	242	57	442	504	838	59	14	213
2	21	125	47	416	462	720	98	40	71
3	25	177	75	417	466	856	81	82	179
4	20	134	30	286	341	642	46	39	165
5	20	220	114	485	467	941	35	79	174
6	22	233	83	438	499	886	54	42	157
7	23	208	82	449	543	864	57	38	21
8	23	135	72	417	439	858	26	39	54
9	23	147	69	451	470	840	54	43	132
10	22	240	29	328	386	633	81	77	145
11	22	118	137	531	552	1107	57	49	99
12	22	235	128	508	538	1063	30	42	80
13	21	223	87	461	500	829	80	64	230
14	22	150	62	394	427	818	58	61	223
15	23	220	135	607	638	1065	93	56	150
16	22	181	107	462	479	946	47	74	119
17	23	102	71	444	490	885	60	33	188
18	22	167	104	461	521	907	99	88	159
19	21	250	33	338	436	690	98	40	180
20	23	179	84	443	505	837	75	84	108
21	24	179	49	438	438	764	34	50	188
22	21	217	64	404	449	757	90	96	138
23	20	240	79	404	442	803	45	61	232
24	21	234	144	569	611	1058	98	87	121
25	25	189	121	569	607	1058	54	55	165
26	23	122	96	473	523	914	80	97	61
27	23	178	139	562	613	1089	71	69	232
28	21	134	141	500	539	1050	29	95	149
29	20	138	92	458	478	794	85	87	216

Продовження таблиці 2.1

№	Х₁	Х₂	Х₃	Х₄	Х₅	Х₆	Х₇	Х₈	Х₉
30	20	203	146	554	592	1098	51	44	140
31	24	185	120	574	621	1071	90	68	13
32	24	113	26	392	467	714	53	11	32
33	25	240	103	441	512	988	47	72	26
34	25	169	40	402	489	752	81	23	233
35	22	172	93	495	481	896	65	81	206
36	24	240	145	614	652	1148	82	38	244
37	25	231	44	399	441	738	59	89	160
38	25	213	103	505	540	1015	46	40	101
39	24	212	88	505	573	952	84	22	127
40	25	152	50	462	485	806	61	37	89

2.3.3 Розраховуємо кореляційну матрицю ( у формі нижньої трикутної матриці) за допомогою програми “Пакет аналіза – Корреляция”. Надаємо границі комірок і позначення рядків та стовпців.

2.3.4 Розраховуємо критичне значення модуля коефіцієнта кореляції:

а) Задаємо рівень значимості  і кількість ступенів воли k по формулі :

k = n-2 (2.1) (2.1)

де n – кількість точок.

б) За допомогою статистичної функції СТЬЮДРАСПОБР() розраховуємо t – критерій при заданих рівні значимості і кількості ступенів волі.

в) Для знаходження критичного значення r розв’язуємо рівняння для критичної точки:

. (2.2)

Для цього перепишемо його у виді:

. (2.3)

Для рішення використовуємо програму Excel “Подбор параметра”

Результаті розрахунку оформляємо у виді таблиці (рис. 2.1).

г) Виділяємо і вказуємо значимі коефіцієнти парної кореляції.

Як випливає з результатів, наявні такі значимі кореляції:

між Х₃ та Х₄ (r = 0,884)		між Х₄та Х₅ (r = 0,940)
між Х₃ та Х₅(r = 0,820)		між Х₄та Х₆(r = 0,918)
між Х₃ та Х₆(r = 0,953)		між Х₅ та Х₆(r = 0,879)

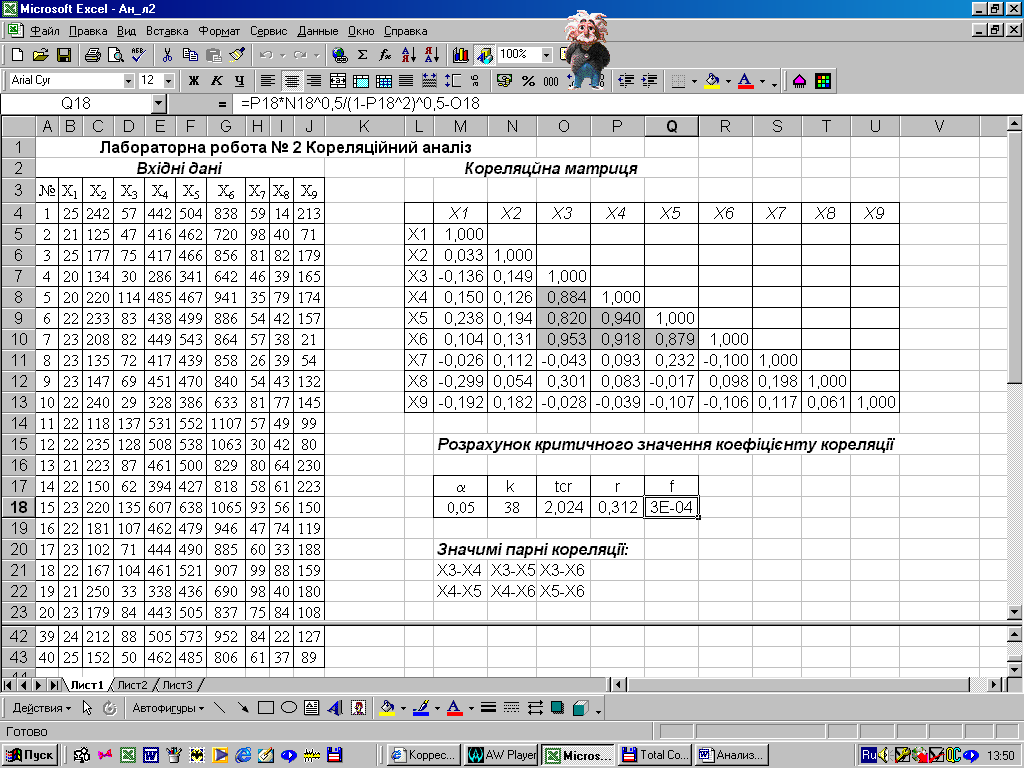
Рисунок 2.1

2.3.5 Будуємо точкові графіки кореляційних полів, переконуємося, що в усіх випадках спостерігається групування точок навколо прямих. Оскільки кореляція відображає силу лінійного зв’язку між перемінними, з наявності кореляції між Х₃ та Х₄,Х₅,Х₆ (рис. 2.2) випливає наявність кореляції між Х₄ та Х₅,Х₆, а також між Х₅ та Х₆

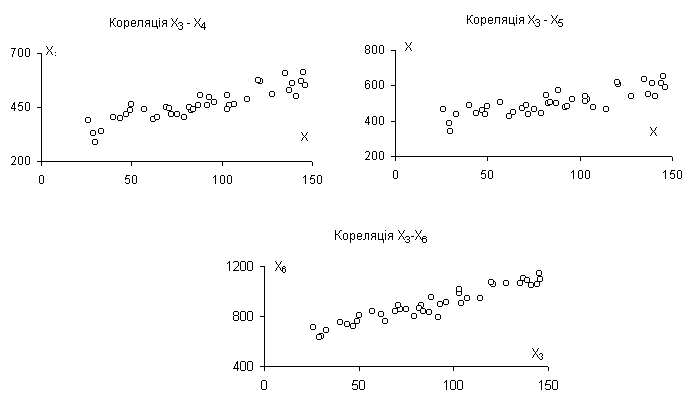
Рисунок 2.2 – Кореляції між Х₃ та Х₄,Х₅,Х₆

2.3.6 Побудова частинних коефіцієнтів кореляції.

Розрахункова формула (для перемінних i та j):

, (2.4)

(k  {i,j})

де R_ij – алгебраїчне доповнення елемента _ij у кореляційній матриці.

Порядок проведення розрахунків:

б) Доповнити нижню трикутну кореляційну матрицю до повної квадратної матриці (наприклад, копіюванням у верхню частину симетричних елементів з піддіагональної частини)

в) Для кожної з пар елементів (i,j):

1) Копіюємо кореляційну матрицю, вирізаємо з неї і-тий рядок та j-й стовпець, розраховуємо одержаний визначник меншого розміру

2) Проводимо аналогічно розрахунки з матрицями і,і та j,j.

3) Розраховуємо частинні коефіцієнти кореляції по формулі (2.4)

4) Результати поміщуємо у таблицю (матрицю)

Примітка. Оскільки така таблиця симетрична відносно головної діагоналі, то при розрахунках можна обмежитися тільки верхньою частиною.

Для створення таблиці бажано створити макрос, якій б розраховував алгебраїчні доповнення.

2.3.7 Порівняльні результати. Порівняємо між собою кореляційну матрицю і матрицю частинних кореляцій (таблиці 2.2 і 2.3). З порівняння випливає, що ті парні кореляції, що були значимі у першому випадку, не є такими у випадку частинних кореляцій, тобто, наявність першої кореляції є пов’язаною із структурою даних (наявністю інших перемінних)

Таблиця 2.2 – Кореляційна матриця (наддіагональна частина)

	Х₁	Х₂	Х₃	Х₄	Х₅	Х₆	Х₇	Х₈	Х₉
Х₁	1,000	0,033	-0,136	0,150	0,238	0,104	-0,026	-0,299	-0,192
Х₂		1,000	0,149	0,126	0,194	0,131	0,112	0,054	0,182
Х₃			1,000	0,884	0,820	0,953	-0,043	0,301	-0,028
Х₄				1,000	0,940	0,918	0,093	0,083	-0,039
Х₅					1,000	0,879	0,232	-0,017	-0,107
Х₆						1,000	-0,100	0,098	-0,106
Х₇							1,000	0,198	0,117
Х₈								1,000	0,061
Х₉									1,000

Таблиця 2.3 – Матриця частинних кореляцій

	1	2	3	4	5	6	7	8	9
1	1,000	0,048	0,884	0,013	-0,499	0,757	0,423	0,700	-0,183
2		1,000	0,057	0,239	0,217	0,066	-0,070	-0,034	0,238
3			1,000	0,050	-0,431	0,908	0,375	0,825	-0,264
4				1,000	0,566	-0,063	-0,165	-0,105	-0,481
5					1,000	-0,192	-0,747	-0,603	0,349
6						1,000	0,083	0,665	-0,244
7							1,000	0,561	-0,266
8								1,000	-0,288
9									1,000

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.201610.76 Mб92000281655.pdf
#
04.12.2018387.58 Кб902.DOC
#
04.12.2018574.98 Кб2403.DOC
#
14.11.2019964.1 Кб90379122_2142C_arhipova_s_p_mayboroda_g_ya_socia...doc
#
04.12.2018167.94 Кб1105.DOC
#
01.05.20251.39 Mб008_lb_AD.doc
#
14.02.20161.13 Mб19510.pdf
#
10.11.201894.72 Кб1211-13.doc
#
01.03.202564.86 Кб21Ponyattya_okhoroni_pratsi.docx
#
25.09.2019329.73 Кб92012_07_02-04_chu_sered_yunakiv_polozhennya.doc
#
12.07.2019142.34 Кб65.doc