Примеры решения задач Пример 1

Определим эквивалент и эквивалентную массу меди в оксидах Cu₂O и CuO.

В оксиде Cu₂O  медь одновалентна; M (Cu)=64 г/моль

Э(Cu)=1 моль, m_э(Cu)= =64 г/моль

В оксиде CuO  медь двухвалентна, значит

Э(Cu)= моль, m_э(Cu)= =32 г/моль

Эквивалентная масса сложного вещества равна сумме эквивалентных масс его составных частей. Составными частями молекулы в этом случае следует считать те ее части, которые в неизменном виде переходят из исходных веществ в продукты реакции. Например, эквивалентная масса оксида состоит из эквивалентной массы металла или неметалла и кислорода:

m_э (оксида)=m_э (металла)+m_э (кислорода) (1.12)

Эквивалентная масса соли состоит из эквивалентной массы металла и эквивалентной массы кислотного остатка:

m_э (соли)=m_э (металла)+m_э (кислотного остатка) (1.13)

Эквивалентная масса кислотного остатка равна его молярной массе, деленной на заряд кислотного остатка.

Между массой вещества и его эквивалентной массой существует зависимость:

m=n_эm_э , (1.14)

где m  масса вещества; n_э  количество эквивалентов вещества; m_э  эквивалентная масса вещества.

Между количеством и числом эквивалентов данного вещества существует зависимость:

n_э=n/Э, (1.15)

где n  количество вещества; n_э  число эквивалентов вещества; Э  эквивалент вещества.

Примеры решения задач Пример 1

Сколько эквивалентов содержится в 450 г MgSO₄?

Решение. По формуле (1.11) вычислим эквивалентную массу сульфата магния:

m_э(MgSO₄)=

Воспользовавшись формулой (1.15), рассчитаем число эквивалентов:

n_э= =7,5 моль

Пример 2

Сколько грамм составляют 7 эквивалентов AgNO₃?

Решение. По формуле (1.11) вычислим эквивалентную массу нитрата серебра:

m_э(AgNO₃)= =170 г/моль

Преобразовав формулу (1.14), рассчитаем массу соли:

m=n_эm_э=7170=1190 г

Упражнения

1. Найдите значение эквивалента гидроксида кальция.

2. Сколько эквивалентов содержится в 320 г CuSO₄?

3. Вычислите эквиваленты и эквивалентные массы H₂SO₄ и Al(OH)₃ в реакциях, выраженных уравнениями: a) H₂SO₄+KOH=KHSO₄+H₂O; б) H₂SO₄+Mg=MgSO₄+H₂; в) Al(OH)₃+HCl=Al(OH)₂Cl+H₂O; г) Al(OH)₃+3HNO₃=Al(NO₃)₃+3H₂O

4. Одно и тоже количество металла взаимодействует с 0,2 г кислорода и с 3,2 г галогена. Вычислите эквивалентную массу галогена.

5. В реакцию с магнием вступило три эквивалента кислорода. Сколько граммов оксида магния образовалось?

2. Способы выражения концентраций

Количество вещества, растворенного в заданном количестве растворителя или раствора, выражают через концентрацию. Концентрацию раствора можно охарактеризовать качественно или количественно. Для качественного описания концентрации используются такие понятия, как разбавленный и концентрированный раствор. О растворах, с относительно низкой концентрацией растворенного вещества, принято говорить, как о разбавленных, а о растворах, с относительно высокой концентрацией,  как о концентрированных.

Компонент раствора, физическое состояние которого сохраняется при образовании раствора, принято считать растворителем. Например, при смешении хлорида натрия (твердое вещество) с водой получается жидкий раствор. Поэтому воду считают растворителем, а NaCl  растворенным веществом. Если все компоненты раствора находятся в одинаковом физическом состоянии, то компонент, присутствующий в большем количестве, считается растворителем.

2.1 Молярную концентрацию раствора определяют как число молей вещества, растворенного в литре раствора:

С_м=

Например, в каждом литре 1,50 молярного раствора (пишется 1,50 М) содержится 1,50 моля растворенного вещества. Чтобы приготовить один литр 0,150 М раствора сахарозы C₁₂H₂₂O₁₁ в воде, нужно взять 0,150 моля С₁₂H₂₂O₁₁. Это количество твердой сахарозы (51,3 г) сначала растворяют в менее чем одном литре воды, а затем полученный раствор разбавляют до окончательного объема 1 л. С этой целью обычно пользуются мерной колбой, имеющей метку, в которую можно налить точно известный объем жидкости.

С помощью молярной концентрации объем можно перевести в моли или моли в объем:

а) вычислить число молей HNO₃ в 2 л 0,200 М раствора HNO₃.

n (HNO₃)=2,0 л раствора0,200 =0,40 моля HNO₃

б) вычислить объем 0,30 М раствора HNO₃, в котором содержится 2,0 моля HNO₃:

V (раствора)=2,0 моля =6,7 л раствора

Пример

Сколько граммов Na₂SO₄ требуется для приготовления 350 мл раствора Na₂SO₄ c концентрацией 0,50 М?

Решение. С_м (Na₂SO₄)= .

Следовательно, n (Na₂SO₄)=0,350 л раствора0,50 =0,175 моля Na₂SO₄.

Поскольку один моль Na₂SO₄ имеет массу 142 г, т.е. М (Na₂SO₄)=142 г/моль, то m (Na₂SO₄)=nM=0,175142=24,8 г

2.2 Процентная концентрация

С_р= 100, %

Пример

Приготовлен раствор, содержащий 6,9 г NaHCO₃ в 100 г воды. Какова процентная концентрация растворенного вещества в этом растворе?

Решение.

С_р= 100= 100=6,5%

Масса раствора  это сумма масс растворителя и растворенного вещества.

3.2 Мольная доля компонента раствора (Х) определяется уравнением:

Х=

Сумма мольных долей всех компонентов раствора должна быть равна 1.

Пример

Вычислите мольную долю HCl в растворе соляной кислоты, содержащем 36 % HCl по массе.

Решение. Допустим, что имеется 100 г раствора (если исходить из какого-то другого количества раствора, то конечный результат будет тем же; это легко проверить, но расчет усложнится). Тогда в растворе должно содержаться 36 г HCl и 64 г H₂O.

n(HCl)= = =0,99 моля

n(H₂O)= =3,6 моля

Х(HCl)= = =0,22.

4.2. Моляльная концентрация или моляльность раствора определяется как число молей растворенного вещества в кг растворителя, а размерность этой концентрации обозначается Мл.

C_g=

Следует обратить внимание на различия между молярностью и моляльностью: при определении моляльности используется масса растворителя, при определении молярности – объем раствора. В растворе, моляльность которого равна 1,50, т.е. в 1,50 Мл растворе содержится 1,50 моля растворенного вещества на каждый кг растворителя. Если растворителем служит вода, моляльность и молярность разбавленного раствора численно почти совпадают, потому что 1 кг растворителя представляет собой почти то же самое, что и 1 кг раствора, а объем 1 кг водного раствора приблизительно равен 1 л.

Пример 1

Раствор какой моляльности получается при растворении 5,0 г толуола (C₇H₈) в 225 г бензола (С₆Н₆).

Решение. ;

.

Пример 2

Исходя из того, что плотность раствора, содержащего 5,0 г толуола и 225 г бензола, равна 0,876 г/мл, вычислите концентрацию этого раствора, выразив ее как: а) молярную концентрацию; б) мольную долю растворенного вещества; в) процентную концентрацию растворенного вещества.

Решение. а) суммарная масса раствора равна массе растворителя плюс масса растворенного вещества:

m_{раствора}=5,0+225=230 г.

Зная массу раствора и его плотность, можно вычислить объем раствора:

V_{раствора}= = =263 мл = 0,263 л.

Сведения о плотности раствора нужны для того, чтобы связать между собой его молярность и моляльность, поскольку первая выражается через объем, а вторая  через массу. Кроме того, чтобы вычислить молярность и моляльность раствора, необходимо знать число молей растворенного в нем вещества:

n(C₇H₈)= = =0,054 моля.

Молярность раствора равна числу молей вещества, растворенного в 1 л раствора:

С_м= = =0,21 М.

б) для вычисления мольной доли растворенного вещества, рассчитаем количество молей каждого из компонентов раствора:

n(C₆H₆)= = =2,88 моля, n(C₇H₈)=0,054 моля.

Мольную долю растворенного вещества вычислим по следующей формуле:

X(C₇H₈)=

в) поскольку процентная концентрация растворенного вещества равна отношению массы растворенного вещества к суммарной массе раствора, то:

C_p=

2. Нормальная концентрация или нормальность раствора (обозначается буквой н.) определяется числом эквивалентов вещества, растворенного в 1 л раствора.

С_н=

Нормальная концентрация раствора всегда представляет собой целое число, кратное молярной концентрации раствора. В окислительно-восстановительных реакциях целочисленный коэффициент пропорциональности между молярностью и нормальностью раствора равен числу электронов, присоединяемых или теряемых одной формульной единицей вещества. В кислотно-основных реакциях этот целочисленный множитель равен числу ионов Н⁺ или ОН^-, которые создаются одной формульной единицей вещества.

Пример

Каковы молярная и нормальная концентрации раствора H₂SO₄, приготовленного растворением 5.00 г H₂SO₄ в таком количестве воды, чтобы получилось 200 мл раствора?

Решение. 1) М(H₂SO₄)=98 г/моль; 2) ;

3) .

Так как одна молекула H₂SO₄ дает два иона водорода, в одном моле этой кислоты содержится 2 химических эквивалента, и поэтому нормальность раствора вдвое превышает его молярность, т.е. равна 0,510н.

1) Э(H₂SO₄)= ; 2) ; 3) C_н=

6.2 Титр определяется количеством грамм вещества, растворенным в 1 мл раствора.

Т= , г/мл

7.2 Равновесная концентрация

Если реагенты и продукты реакции находятся во взаимном контакте, химическая реакция может достичь состояния динамического равновесия, в котором прямая и обратная реакции протекают с одинаковыми скоростями. Это состояние называется химическим равновесием. Свойства равновесной системы не меняются с течением времени. Для такой системы отношение произведения концентраций всех продуктов к произведению концентраций всех реагентов, каждая из которых возведена в степень, равную стехиометрическому коэффициенту данного участника реакции в ее полном химическом уравнении, называется константой равновесия К.

jA+kB pC+qD

K= (7.2.1)

Константа равновесия зависит от температуры, но на нее не влияют не изменения относительных концентраций реагирующих веществ, ни давление в реакционной системе, ни наличие в ней катализатора.

При использовании молярных концентраций константу равновесия обозначают символом К_с, а при измерении концентраций парциальными давлениями (в атмосферах) константу равновесия обозначают символом К_р.

jA+kB dAB

K_p= (7.2.2)

Константы К_с и К_р связаны между собой соотношением:

K_p=K_c(RT) , (7.2.3)

где  изменение числа молей газа в реакции.

Большое значение константы равновесия указывает на то, что в равновесной смеси должно содержаться больше продуктов, чем реагентов. Малая величина константы равновесия означает, что равновесие сдвинуто в сторону реагентов.

Пример

В одном из экспериментов немецкий химик Фриц Габер и его сотрудники в начале XX века вводили в реакционный сосуд смесь водорода и азота, а затем ждали, пока в системе не установится равновесие при 472°С. После анализа в равновесной смеси газов было обнаружено 0,1207 М Н₂, 0,0402 М N₂ и 0,00272М NH₃. Вычислите по этим данным константы равновесия К_с и К_р реакции:

N_2(г.)+3Н_2(г.) 2NH_3(г.)

Решение. а) К_с=

б) в этой реакции из 4 молей газообразных реагентов (1N₂+3H₂) образуется 2 моля газообразных продуктов (2NH₃). Следовательно, n=24= 2 (любую величину, обозначаемую символом , всегда получают вычитанием из результата, в рассматриваемом случае данных для продуктов, исходного значения, т.е. данных для реагентов).

Абсолютная температура эксперимента Т=273+472=745 К

Воспользуемся значением универсальной газовой постоянной R=0,0821 .

К_р=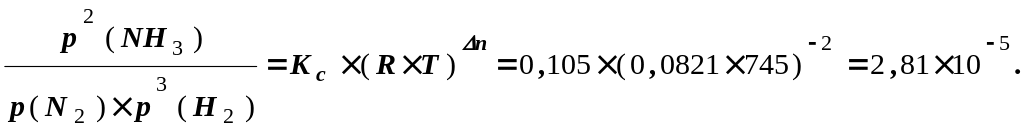

При вычислении констант равновесия соответствующие концентрации можно подставлять вместе с единицами измерения, и тогда константа равновесия К приобретет определенную размерность. Например, для реакции N₂O_(г.) 2NO_2(г.) имеем К= Если в данном случае концентрацию веществ выразить в молях, константа равновесия примет размерность , а если концентрацию выразить в атмосферах, константа равновесия имеет размерность Выражая константы равновесия в единицах определенной размерности, мы тем самым указываем и единицы, в которых выражены концентрации, а это имеет свои удобства. Тем не менее чаще константы равновесия записывают как безразмерные величины.

7.2.1. Гетерогенные равновесия

Во многих важных равновесных системах все вещества находятся в одинаковом фазовом состоянии. Такие равновесные системы называются гомогенными. Но равновесие может устанавливаться и между веществами, которые находятся в разных фазовых состояниях, и в таком случае говорят о гетерогенном равновесии. В качестве примера рассмотрим разложение карбоната кальция:

CaCO_3(тв.) СаО_(тв.)+СО_2(г.)

В этой системе газ находится в равновесии с двумя твердыми веществами. Если написать выражение для константы равновесия так, как мы это делали до сих пор, то получим:

K= .

Так как карбонат и оксид кальция присутствуют в системе в виде твердых веществ, их концентрации остаются постоянными. Число молей твердого вещества, приходящееся на литр его объема, не зависит от того, много или мало этого вещества имеется в системе. Концентрацию чистого жидкого или твердого вещества можно выразить через отношение плотности к молекулярной массе:

Плотность чистого жидкого или твердого вещества при любой заданной температуре постоянна, а при изменении температуры меняется очень незначительно. Поэтому можно с удовлетворительной точностью считать эффективную концентрацию чистого жидкого или твердого вещества постоянной. С практической точки зрения результат этой продцедуры эквивалентен тому, как если бы мы в выражении для константы равновесия условно приняли концентрации твердых веществ равными единице.

K=[CO₂]

Пример

Напишите выражение для константы равновесия каждой из следующих реакций:

1. CO_2(г.)+Н_2(г.) СО_2(г.)+Н₂О_(ж.)

б)SnO_2(тв.)+2СО_(г.) Sn_(тв.)+2СО_2(г.)

Решение. а) поскольку вода участвует в данной реакции в виде чистой жидкости, ее концентрацию не следует включать в выражение для константы равновесия:

K=

б) поскольку SnO₂ и Sn являются чистыми твердыми веществами, они не входят в выражение для константы равновесия:

K=

7.2.2 Кажущаяся константа равновесия

Допустим, что смесь 2,0 моля Н₂, 1,00 моля N₂ и 2,00 моля NH₃ поместили в сосуд объемом 1 л при температуре 472 К. Будет ли реакция между N₂ и Н₂ давать дополнительное количество NH₃? Подставив начальные концентрации N₂, H₂ и NH₃ в выражение для константы равновесия реакции, найдем:

K =

В примере раздела 7.2 было установлено, что при заданной температуре К_с=0,105. Следовательно, для того чтобы система приблизилась к равновесию,

отношение должно уменьшиться с 0,500 до 0,105. Это произойдет при уменьшении [NH₃] и увеличении [N₂] и [H₂]. Следовательно, по мере образования N₂ и Н₂ из NH₃ реакция будет смещаться в сторону установления равновесия, другими словами, реакция должна протекать справа налево.

Подставляя произвольные концентрации реагентов и продуктов в выражение для константы равновесия, мы получим кажущуюся константу равновесия, которую обозначают буквой Q. Кажущаяся константа равновесия становится равной истинной константе равновесия К только тогда, когда концентрации всех компонентов реакционной системы достигнут своих равновесных значений, т.е. Q=K только при равновесии. Если кажущаяся константа равновесия больше К, то вещества, указанные в правой части химического уравнения реакции, должны реагировать с образованием веществ, указанных в его левой части, другими словами, реакция приближается к равновесному состоянию, смещаясь справа налево. Следовательно, если Q>K, реакция сдвигается справа налево. И наоборот, если Q<K, реакция приближается к равновесному состоянию с образованием дополнительного количества продуктов (смещается слева направо).

7.2.3 Вычисление равновесных концентраций

Если нам известна константа равновесия некоторой реакции, то мы можем вычислить концентрации веществ в реакционной смеси при равновесии. Сложность такого расчета зависит от нескольких факторов: сложности химического уравнения реакции и от того, какие концентрации уже известны. Общий характер подобных расчетов станет понятен после решения следующих примеров.

Пример 1

При каком парциальном давлении NH₃ находится в равновесии с N₂ и Н₂ при 500°С, если равновесное парциальное давление Н₂ равно 0,733 атм., а N₂ 0,527 атм. При 500°С для реакции N_2(г.)+3Н_2(г.) 2NH_3(г.) константа равновесия К_р=1,45 10^-5.

Решение. К_р=

Поскольку значения К_р, р(N₂) и р(Н₂) заданы, из выражения для константы равновесия можно найти р(NH₃):

p²(NH₃)=K_p (1,45 ,

откуда р(NH₃)=