2.4.1 Расчет рабочих лопаток на статическую прочность и колебания Особенности расчета при использовании программы prokol.

Расчет производится на ПК методом конечных разностей с помощью программы PROKOL [6], [47]. Перо лопатки сплошное и по длине разбивается пятью сечениями на четыре равные части. Нулевое сечение совмещается с концевым, а четвертое – с втулочным сечением лопатки. По результатам расчета строятся графики распределения параметров по длине (от номера сечений) лопатки:

- напряжений растяжения от центробежных сил, МПа;

, , - напряжений изгиба в точках А, В, С профилей, МПа;

, , - суммарных напряжений в точках А, В, С профилей, МПа;

- максимальных суммарных напряжений в сечении, МПа,

- температуры лопатки в сечении, К;

- предельных напряжений в сечении, МПа;

- коэффициентов запаса прочности в сечении.

Следует помнить, что данный метод расчета не учитывает термических напряжений, возникающих от градиента температур по длине пера лопатки.

Для компрессорных лопаток влияние температуры на величину обычно невелико. Считают, что = , = .

Для сплошных лопаток турбины максимальное значение температуры обычно располагается на двух третях ее длины, то есть между 3 и 4 сечениями.

Распределение температуры по длине лопатки определяется формой радиальной эпюры газа и отводом тепла в охлаждаемый диск. Форма радиальной эпюры выбирается такой, чтобы обеспечить прочностную надежность (запасы прочности) в опасных сечениях вблизи втулочного сечения и сохранить минимальный радиальный зазор между ротором и статором. С этой целью температуру газа у концевого и втулочного сечений лопатки первой ступени снижают, что приводит к уменьшению радиальных деформаций статора и сохранению повышенных предельных напряжений материала лопатки. Однако, эта эпюра радиального распределения температуры в последующих ступенях, к сожалению, выравнивается.

Снижение температуры втулочного сечения сплошной лопатки за счет отвода тепла в охлаждаемый диск происходит на 100…150 К для двигателей первого-третьего поколений, на 200…250 К у двигателей четвертого поколения (в зависимости от типа системы охлаждения и расхода охлаждающего воздуха). У двигателей пятого поколения ( = 1600…1700 К) снижение температуры лопатки за счет охлаждения еще больше. При этом максимальная температура лопатки не превышает 1150 К.

Для приближенной оценки распределения температурного поля первой ступени турбины и предельных напряжений по длине лопатки можно воспользоваться таблицей 1.

Таблица 1 – Распределение температуры и предельных напряжений по длине лопатки

	0	1	2	3	4
	0.95	1.06	1.06	1.0	0.8
, К
, МПа

В таблице приняты следующие условные обозначения:

- номер сечения лопатки;

- температура газа в сечении, К;

- среднемассовая температура газа, К;

=(0.90…0.95) - температура лопатки в сечении, К.

Величины предельных напряжений для различных температур могут быть найдены в работах [3], [6, с. 288].

В конце этого раздела на основании сравнения рассчитанных запасов прочности с нормативными, делается заключение о работоспособности, массе и прочностной надежности рабочей лопатки.

Особенности расчета при использовании конечно-элементного пакета ANSYS.

Построение модели и метод расчета приведены в работе [***]. Для построения параметрической модели лопатки вводятся координаты точек, описывающих ее втулочное, среднее и периферийное сечение. Входная и выходная кромки моделируются в виде трапеций (точки 1, 2, 3, 4, рисунок 4), корытце и спинка описываются точками вписанных в профиль окружностей (точки 5, 6 и так далее). Для каждой пары точек создается своя локальная система координат, позволяющая легко изменять толщину профиля.

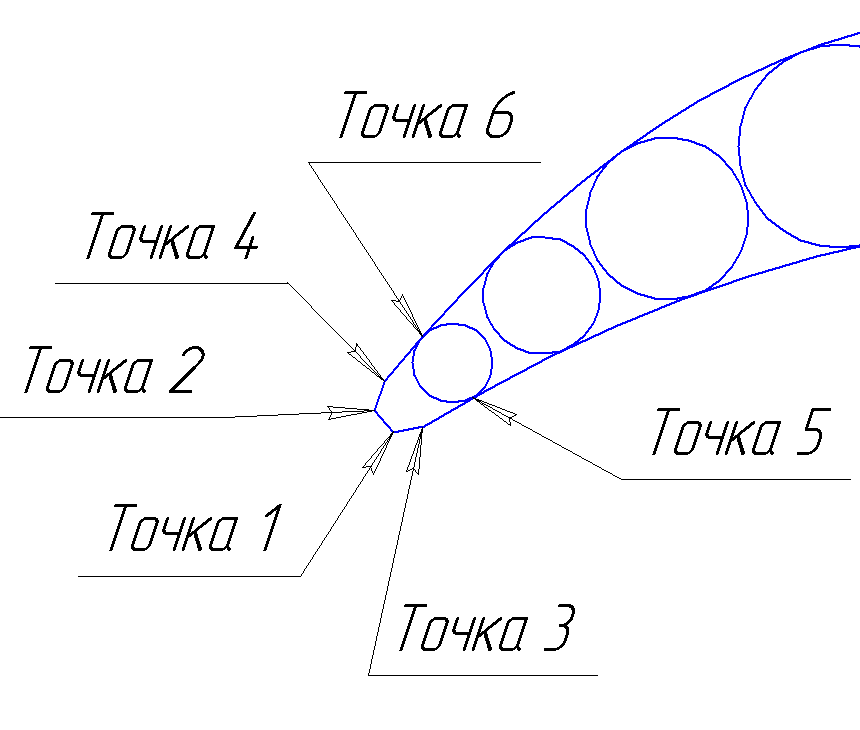
Рисунок 4 – точки сечения лопатки

Определяются координаты центра тяжести каждого профиля, затем, при помощи добавления к координатам противоположных по знаку величин, все три центра тяжести располагаются вдоль оси Z. Строится объемная модель пера лопатки и разбивается на конечные элементы типа Solid 45 так, чтобы по толщине лопатки было не менее 3 конечных элементов, и форма элементов приближалась к кубу. Газовая нагрузка прикладывается к корытцу лопатки, для чего там создаются элементы поверхностного эффекта Surf 154, допускающие приложение давления под углом к поверхности. Лопатка нагружается также угловой скоростью вращения.

Для расчета коэффициентов запаса используются осевые напряжения лопатки - SZ. Для вывода результатов по отдельному сечению используется операция вывода значений по пути Path Operations (рисунок 5).

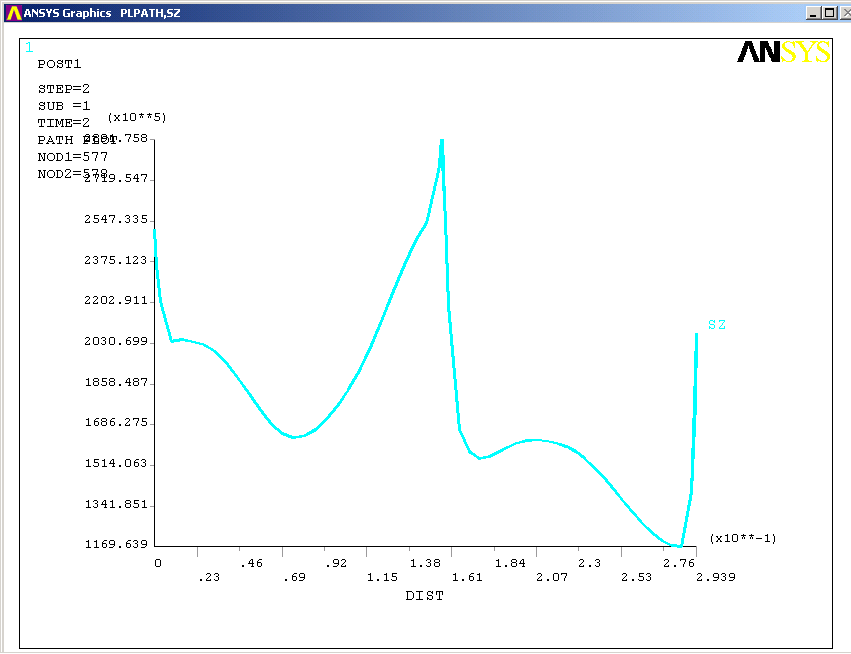
Рисунок 5 – напряжения по сечению лопатки

Для разгрузки лопатки от напряжений изгиба производится вынос центров тяжести сечений. Простейший закон выноса – линейный, при этом изменение координат центра тяжести корневого сечения равно нулю, а среднего сечения – половине изменения координат периферийного сечения. Необходимо провести исследование зависимости напряжений в лопатке от выноса центра тяжести. Для этого вначале производится вынос центра тяжести по шагам в направлении оси Х, и определяется оптимальное значение выноса по оси Х, при котором напряжение минимально. Затем это значение фиксируется, и производится поиск оптимума по оси Y.

Если вынос центра тяжести сечения не обеспечил нормативного запаса прочности лопатки, необходимо утолстить ее сечения.

В пояснительную записку включаются:

- модель лопатки, разбитая на конечные элементы;

- расчет газовой нагрузки;

- графики зависимости напряжений от выноса центра тяжести сечений;

- распределение напряжений по перу лопатки;

- распределение напряжений по сечению лопатки.

На основании сравнения рассчитанных запасов прочности с нормативными, делается заключение о работоспособности, массе и прочностной надежности рабочей лопатки.

Расчет рабочей лопатки на колебания сводится к оценке ее вибрационного состояния и построения резонансной диаграммы ступени для различных режимов работы двигателя – от малого газа до максимального. Резонансная диаграмма ступени представляет собой зависимость собственной частоты лопатки от секундной частоты вращения (частотная диаграмма), на которую нанесены лучи гармоник возбуждения (диаграмма возбуждения). Точки пересечения этих диаграмм определяют опасные гармоники и частоты вращения, при которых возникают резонансные колебания лопатки.

Построение резонансной диаграммы ступени начинается с расчета на ПК собственной статической частоты первой изгибной формы методом наложений по формуле А.Е.Шнейдмана [18], [47]. В распечатке значение этой частоты определено для не вращающегося ротора, поэтому она называется статической.

Собственная статическая частота не учитывает влияния центробежных сил и температуры нагрева лопатки, возникающих при работе двигателя. Для учета этих влияний можно воспользоваться приближенным выражением

= ,

где - динамическая собственная частота лопатки, Гц;

, - модули упругости материала лопатки при нормальной и рабочей температурах, МПа;

- секундная частота вращения ротора, ;

= 0,81 - 0,37 - Cоs - постоянный коэффициент, зависящий от геометрии пера лопатки;

- средний диаметр лопатки, м;

- длина лопатки, м;

- средний угол закрутки по длине лопатки, град.

Центробежная сила выпрямляет линию прогибов лопатки, изгибная жесткость ее растет и собственная частота увеличивается.

Для лопаток компрессора влияние температуры на модуль упругости незначительно , поэтому, с ростом частоты вращения динамическая собственная частота лопатки будет увеличиваться.

Для лопаток турбины с повышением частоты вращения от режима малого газа до максимального динамическая собственная частота рабочей лопатки несколько снижается за счет падения модуля упругости материала из-за роста температуры.

Для приближенной оценки температуры в среднем сечении лопатки на рабочих режимах работы двигателя при оборотах от малого газа n_cмг до максимального можно воспользоваться зависимостью

= ,

где - температура газа при частоте вращения ротора , К;

- температура воздуха в стандартных атмосферных условиях, К;

n_с - секундная частота вращения на текущем режиме работы от малого газа до максимального, ;

- температура газа на максимальном режиме работы двигателя, К.

Следует учесть снижение температуры в сопловом аппарате на 130…150 К, а также влияние системы охлаждения лопатки на ее температуру.

Величины модулей упругости для различной температуры могут быть определены путем линейной аппроксимации их табличных значений. Среднее значение температуры пера лопатки можно приближенно оценить как

= (0.90…0.95)

Построение резонансной диаграммы ступени удобно проводить по расчетным точкам (5…7), используя таблицу 2.

Откладывая по оси абсцисс секундную частоту вращения ротора n_с, а по оси ординат – собственные динамические частоты колебаний лопатки, по точкам строим частотную диаграмму лопатки.

Таблица 2 – Изменение динамической собственной частоты

,
, К
. , МПа
, Гц

Ввиду технологического разброса собственных частот лопаток рабочего колеса, вместо одной кривой изменения этих частот, строятся две – одна с разбросом в плюс 5% от расчетной, другая – в минус 5%. Такая диаграмма называется частотной диаграммой ступени. Предполагается, что между этими кривыми находится поле собственных частот всех лопаток ступени.

Колебания рабочих лопаток возникают вследствие неоднородности потока газа в окружном направлении. Частота возбуждения определяется числом импульсов , получаемых лопаткой за каждый оборот ротора

= ,

где =1, 2, 3, … - номер гармоники возбуждающей силы.

Это выражение для частоты возбуждения представляет собой уравнение прямой – луча, исходящего из начала координат - , а номер гармоники - тангенс угла наклона этого луча.

Обычно номер гармоники возбуждения соответствует числу конструктивных элементов проточной части двигателя (стойки, жаровые трубы, топливные форсунки, лопатки), вносящих возмущения в поток. Места пересечения лучей диаграммы возбуждения с частотной диаграммой ступени определяют резонансы, обусловленные опасными гармониками.

Пример оформления резонансной диаграммы ступени компрессора приведен на рисунке 6.

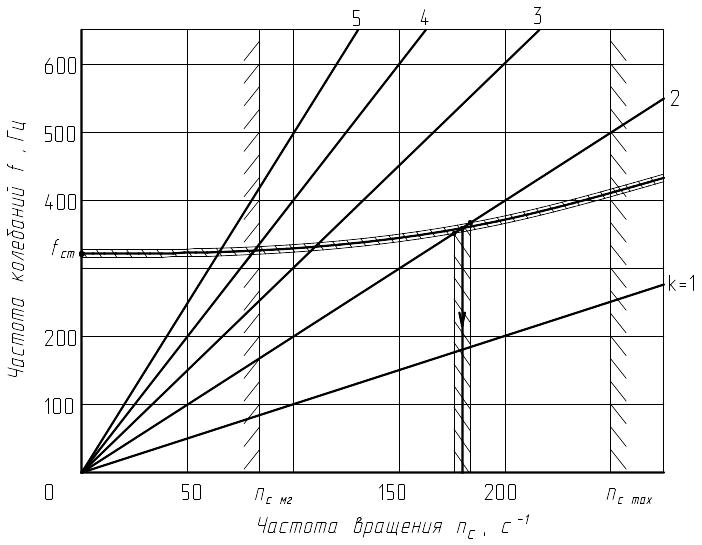
Рисунок 6 - Резонансная диаграмма первой ступени компрессора ВД

В конце этого раздела определяются опасные гармоники и частоты вращения в рабочем диапазоне режимов работы двигателя от малого газа до максимального.

На основании анализа резонансной диаграммы ступени делают предположения о возможных источниках возбуждения и даются рекомендации по обеспечению вибрационной надежности лопатки.

Особенности расчета на колебания при использовании конечно-элементного пакета ANSYS

При построении резонансной диаграммы пакет ANSYS позволяет точно учесть влияние центробежных сил. Для этого предварительно производится статический расчет с включенной опцией расчета нагружения Main Menu>Solution>Analysis Options: prestress on. Далее производится расчет собственных частот и форм колебаний лопатки (модальный анализ). Рассчитываются первые 10 собственных частот. Для классификации формы колебаний отображаются поля суммарных перемещений лопатки (USUM).

Параметрическая модель лопатки, ранее созданная в ANSYS, позволяет исследовать влияние толщины сечения на собственные частоты лопатки. Выбирается одна из частот по указанию преподавателя. Далее корневое, среднее и периферийное сечения последовательно изменяются на +20% и -20% по толщине (при сохранении неизменными всех остальных сечений лопатки).

Результаты этого исследования позволяют провести частотную отстройку лопатки от резонанса. Для этого:

1. Точка резонанса смещается на 10% по оборотам двигателя вверх или вниз от режима продолжительной работы двигателя;

2. Частотная линия лопатки параллельно переносится в новую точку резонанса. При этом видно, насколько необходимо изменить статическую частоту;

3. По результатам исследования влияния толщины сечений на собственную частоту определяется, какое сечение нужно изменить, и насколько, для необходимого изменения статической частоты лопатки;

4. Расчетом подтверждается новая собственная частота лопатки;

5. Так как сечения лопатки изменены, необходим расчет измененного варианта лопатки на статическую прочность.

В пояснительную записку включаются:

- таблица рассчитанных 10 собственных частот и форм колебаний;

- резонансная диаграмма для частоты, указанной преподавателем;

- зависимости собственной частоты от толщины сечений лопатки;

- расчет собственной частоты лопатки после частотной отстройки;

- расчет измененной лопатки на статическую прочность.