
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
- •І рівень
- •Іі рівень
- •І рівень
- •Іі рівень
- •Ііі рівень
Іі рівень
Якщо осьовий переріз циліндра – квадрат, площа якого дорівнює Q, то площа основи циліндра дорівнює:
а) ; б) ; в) ; г) . (1 бал)
Якщо радіус основи циліндра дорівнює R, а висота – 2R , то кут нахилу діагоналі осьового перерізу до площини основи дорівнює:
а) 30°; б) 45°; в) 60°; г) 75°. (1 бал)
Якщо осьовий переріз конуса – правильний трикутник зі стороною 2r, то площа перерізу, проведеного через дві твірні, кут між якими 30°, дорівнює:
а) r2 ; б) r2 ; в) r2; г) 2r2. (1 бал)
Ііі рівень
Якщо в циліндр, осьовий переріз якого – квадрат, вписано правильну чотирикутну призму, то відношення висоти цієї призми до сторони основи дорівнює:
а) : 2; б) 2 : ; в) : 1; г) 1 : . (2 бали)
Якщо в конус, осьовий переріз якого – прямокутний трикутник, вписано правильну чотирикутну піраміду, то відношення більшого ребра піраміди до сторони основи дорівнює:
а) 2: 1; б) : 1; в) 1 : 1; г) 1 : . (2 бали)
Якщо радіуси основ зрізаного конуса дорівнюють 4 і 1 см, а твірна – 5 см, то висота конуса дорівнює :
а) 4 см; б) 5 см; в) 6 см; г) 7 см . (2 бали)
ІV РІВЕНЬ
Якщо через дві твірні конуса, кут між якими дорівнює , проведено переріз, а висота конуса дорівнює R і утворює з його твірною кут , то площа перерізу дорівнює:
а) б)
б)
 ;
в)
;
в)
 ;
г)
;
г)
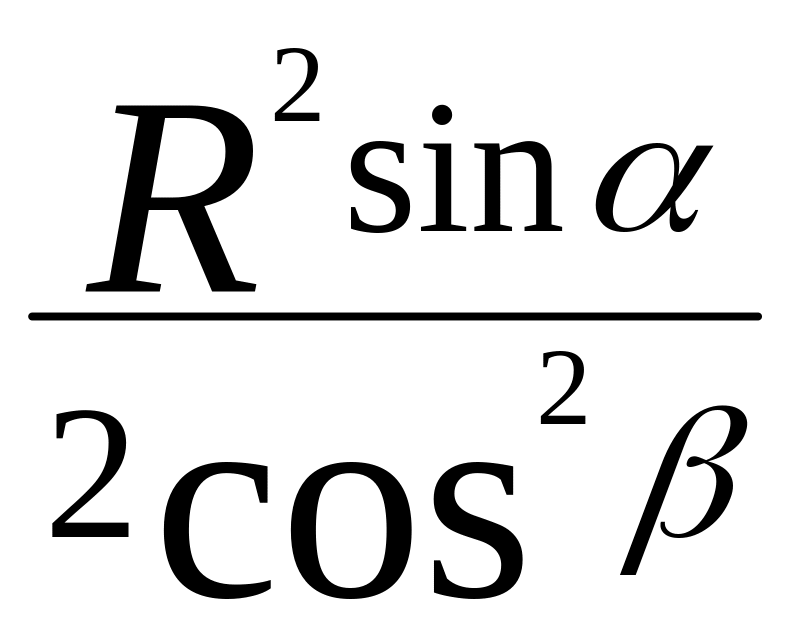 .
(3 бали)
.
(3 бали)
Нехай S(x) – площа перерізу конуса площиною, паралельною основі і віддаленої від неї на відстань х (0<х<Н, де Н – висота конуса), тоді графік залежності у= S(x) подано на рисунку. (3 бали)

у у у у
О а х О б х О в х О г х
Якщо вершини прямокутника лежать на колах основ циліндра, у якого радіус 13 см, а твірна 32 см, і сторони прямокутника відносяться як 1 : 4, то його площа дорівнює:
а) 36 см2; б) 256 см2; в) 400 см2; г) 900 см2. (3 бали)
Таблиця відповідей
Рівень |
Номер завдання |
Варіант 1 |
Варіант 2 |
І |
1 |
г |
в |
2 |
б |
а |
|
3 |
б |
а |
|
ІІ |
1 |
в |
б |
2 |
г |
в |
|
3 |
г |
в |
|
ІІІ |
1 |
в |
б |
2 |
б |
в |
|
3 |
а |
б |
|
ІV |
1 |
в |
г |
2 |
г |
г |
|
3 |
а, г |
б, в |
ВАРІАНТ 1
І рівень
Якщо радіус кулі дорівнює 15 см, а точка А знаходиться від центра кулі на відстані 20 см, то точка А лежить:
а) всередині кулі; б) на поверхні кулі; в) поза кулею; г) визначити неможливо. (1 бал)
Радіус сфери дорівнює R , відстань від центра сфери до деякої площини дорівнює d. Дана площина дотикається сфери, якщо виконується умов:
а) d–R>0;
б) d–R<0;
в) d–R![]() 0;
г) d–R=0.
(1 бал)
0;
г) d–R=0.
(1 бал)
Якщо радіус кулі дорівнює R, то площа великого круга дорівнює:
а) R; б) R2; в)2 R; г) 2 R2. (1 бал)
