Розділ 3. Рівняння, нерівності та їхні системи.
8. Тема 4. Розв‘язування систем ірраціональних рівнянь.
Навчальна мета: Розширити знання про системи рівнянь, про їх види та методи розв‘язування систем нелінійних рівнянь.
План.
Розв‘язування систем ірраціональних рівнянь.
Анотація
Повторіть, приступаючи до вивчення даної теми методи розв‘язування систем рівнянь та методи розв‘язування ірраціональних рівнянь (звільнитись від ірраціональності).
Вправи
Розв’язати систему рівнянь:
1.
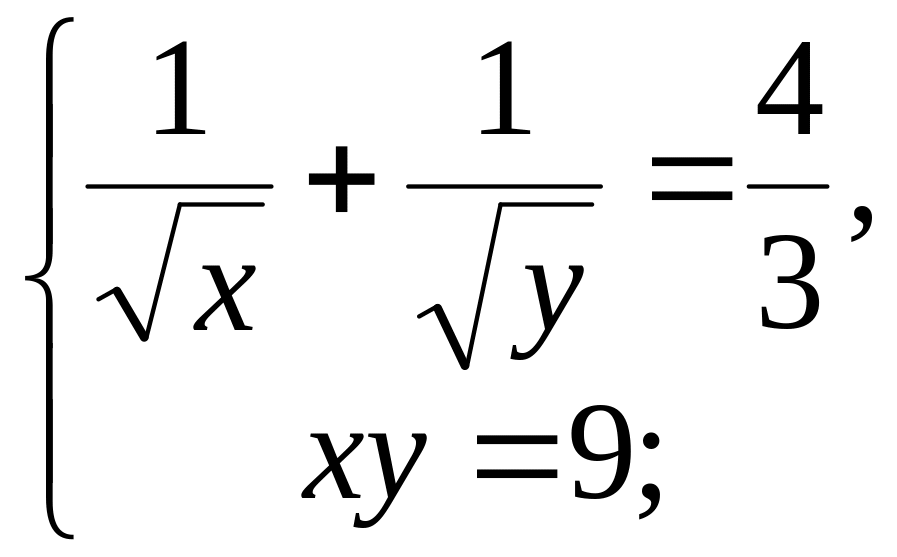
2.
3.
4.
Питання для самоконтролю
Яке рівняння називають ірраціональним?
Які перетворення ірраціональних рівнянь можуть привести до появи сторонніх коренів?
У чому полягає спосіб введення нової змінної під час розв‘язування ірраціональних рівнянь?
Які методи використовуються при розв‘язуванні ірраціональних рівнянь?
У чому полягає спосіб введення нової змінної під час розв‘язування систем ірраціональних рівнянь?
Основна література.
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002, ст..164-168.
Додаткова література.
Бевз Г.П. Алгебра і початки аналізу: Підручник для 10-11 класу загальноосвіт. навч. закл. – К.: Освіта, 2005
9. Тема 5. Системи показникових і логарифмічних рівнянь.
Навчальна мета: Розширити знання про системи рівнянь, про їх види та методи розв‘язування систем показникових і логарифмічних рівнянь.
План.
Розв’язування систем показникових рівнянь.
Розв’язування систем логарифмічних рівнянь.
Анотація
Повторіть, приступаючи до вивчення даної теми методи розв‘язування систем рівнянь та методи розв‘язування показникових та логарифмічних рівнянь.
Вправи
Розв’язати систему рівнянь:
1.
2.
3.
4.
Питання для самоконтролю
Яке рівняння називають показниковим?
Яке рівняння називають логарифмічним?
Яка система рівнянь називається показниковою системою?
Яка система рівнянь називається логарифмічною системою?
У чому полягає спосіб введення нової змінної під час розв‘язування рівнянь?
Які методи використовуються при розв‘язуванні систем рівнянь?
У чому полягає спосіб введення нової змінної під час розв‘язування систем рівнянь?
Основна література.
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник) , 10-11 кл. – К.: Зодіак – ЕКО, 2002, ст. 202-206, 239-242
Додаткова література.
Бевз Г.П. Алгебра і початки аналізу: Підручник для 10-11 класу загальноосвіт. навч. закл. – К.: Освіта, 2005
10. Тема 8. Системи нелінійних рівнянь, їх види, методи розв’язання.
Навчальна мета: Розширити знання про системи рівнянь, про їх види та методи розв‘язування систем нелінійних рівнянь.
План.
Системи нелінійних рівнянь, їх види.
Методи розв’язування систем нелінійних рівнянь.
Анотація
Повторіть, приступаючи до вивчення даної теми методи розв‘язування систем нелінійних рівнянь та методи розв‘язування показникових, логарифмічних, ірраціональних та тригонометричних рівнянь.
Вправи
Розв’язати систему рівнянь:
1.
2.
3.
4.
Питання для самоконтролю
Яке рівняння називають показниковим?
Яке рівняння називають логарифмічним?
Яке рівняння називають ірраціональним?
Які рівняння називають найпростішими тригонометричними рівняннями?
Запишіть формули для розв‘язування найпростіших тригонометричних рівнянь.
У чому полягає спосіб введення нової змінної під час розв‘язування рівнянь?
Які методи використовуються при розв‘язуванні систем рівнянь?
У чому полягає спосіб введення нової змінної під час розв‘язування систем рівнянь?
Основна література.
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002.
Додаткова література.
Бевз Г.П. Алгебра і початки аналізу: Підручник для 10-11 класу загальноосвіт. навч. закл. – К.: Освіта, 2005