V1: Оптимизация динамических систем
V2: Динамические задачи оптимизации
I:
S: Какую особенность имеет динамическое программирование как многошаговый метод оптимизации управления:
+: отсутствие последействия
-: наличие обратной связи
-: управление зависит от бесконечного числа переменных
I:
S: Вычислительная схема метода динамического программирования :
-: зависит от способов задания функций
-: зависит от способов задания ограничений
+: связана с принципом оптимальности Беллмана
I:
S: Какую задачу можно решить методом динамического программирования
-: транспортную задачу
+: задачу о замене оборудования
-: принятия решения в конфликтной ситуации
I:
S: Процесс нахождения решений в задачах динамического программирования является…
-: знакопеременным
-: асимптотическим
-: расходящимся
+: многоэтапным
V1: Оптимизация в условиях неопределенности
V2: Элементы теории матричных игр
I:
S: Платежной матрицей называется матрица, элементами которой являются:
-: годовые прибыли отраслевых предприятий
+: выигрыши, соответствующие стратегиям игроков
-: налоговые платежи предприятий
I:
S: Верхней ценой парной игры является:
-: гарантированный выигрыш игрока А при любой стратегии игрока В
-: гарантированный выигрыш игрока В
+: гарантированный проигрыш игрока В
I:
S: Чистой ценой игры называется:
-: верхняя цена игры
-: нижняя цена игры
+: общее значение верхней и нижней ценой игры
I:
S: Возможно ли привести матричную игру к задаче линейного программирования:
+: возможно
-: невозможно
-: возможно, если платежная матрица единичная
I:
S: Кооперативные игры – это игры:
-: с нулевой суммой
-: со смешанными стратегиями
+: допускающие договоренности игроков
I:
S:
Верхняя цена матричной игры, заданной
платежной матрицей
,
равна …
-: 4
-: 1
-: 2
+: 3
I:
S:
Матричная игра задана платежной матрицей
.
Тогда нижняя цена игры равна…
-: 5
+: 4
-: 8
-: 2
I:
S:
Матричная игра задана платежной матрицей
.
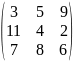Тогда нижняя цена игры равна…
-: 2
-: 3
-: 4
+: 6
V2: Игры с природой
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков:
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
-:
+:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите матрицу рисков.
+:
-:
-:
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий крайнего оптимизма.
-: А1
-: А2
+: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Лапласа (критерий максимального среднего выигрыша).
-: А1
-: А2
-: А3
+: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Вальда.
(Критерий крайнего пессимизма)
-: А1
+: А2
-: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Сэвиджа
(Критерий пессимизма)
-: А1
+: А2
-: А3
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий крайнего оптимизма.
-: А1
-: А2
+: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Лапласа
(критерий максимального среднего выигрыша)
-: А1
-: А2
+: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Вальда (критерий крайнего пессимизма):
-: А1
+: А2
-: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Сэвиджа.
-: А1
+: А2
-: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0.3.
-: А1
+: А2
-: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0.4.
-: А1
-: А2
+: А3
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0.5.
-: А1
-: А2
+: А3
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0,6.
-: А1
+: А2
-: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0,6
-: А1
+: А2
-: А3
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0.7
-: А1
-: А2
+: А3
-: А4
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0.3
-: А1
-: А2
+: А3
I:
S: Имеется следующая матрица выигрышей:
Определите наилучшую стратегию принятия решения, используя критерий Гурвица при соотношении критериев оптимизма/пессимизма =0.4
-: А1
+: А2
-: А3
-: А4
I:
S: Матрица выигрышей в игре с природой имеет вид:
|
|
|
|
4 |
1 |
|
3 |
3 |
|
2 |
5 |
|
1 |
6 |
Тогда средний выигрыш игрока, по критерию Байеса, относительно выигрышей будет равен…
+: 3,1
-: 2,5
-: 3,12
-: 6
I:
S: Матрица выигрышей в игре с природой имеет вид:
|
|
|
|
1 |
6 |
|
3 |
4 |
|
4 |
3 |
|
5 |
2 |
Тогда оптимальной, по критерию Байеса, будет стратегия…
+:
-:
-:
-:
I:
S: Матрица выигрышей в игре с природой имеет вид:
|
|
|
|
2 |
10 |
|
6 |
8 |
|
8 |
4 |
|
12 |
2 |
Тогда средний выигрыш игрока, по критерию Байеса, относительно выигрышей будет равен…
-: 12,0
+: 8,0
-: 4,5
-: 6,5