Основная теорема зацепления.

“ Общая нормаль к профилям зубьев, проходящая через точку их контакта, делит линию центров на части обратно пропорциональные угловым скоростям.”

n

П

n

Для того чтобы передача имела постоянное передаточное отношение, профиль зуба должен быть очерчен такой кривой, чтобы нормаль к профилю зуба в любой момент времени проходила через одну и ту же точку П (полис зацепления).Такому условию удовлетворяют лишь некоторые кривые:

• эвольвента;

• окружность;

• циклоида.

Вмашиностроении наибольшее распространение получии эвольвентные профили зубьев в силу ряда преимуществ:

1. зубья могут нарезаться простым инструментом, имеющим прямолинейный профиль зуба ( зубчатая рейка);

2. каждое колесо может сцепляться с колесом, имеющим любое число зубьев.

3. Эвольвентное зацепление менее чувствительно к отклонениям межосевого расстояния;

4. Допускает улучшение профиля зубьев (коррегирование)

Коррегирование – это улучшение профиля зуба путем его очерчивания другим участком эвольвенты по сравнению с нормальным зацеплением. Выполняется засчет смещения инструмента к центру или от центра заготовки при нарезании зубьев. Смещение инструмента от центра заготовки считается положительным, к центру – отрицательным.

Обозначим (мм) – смещение инструмента , тогда относительное смещение :

При X=0 передачи без смещения.

Коррегирование необходимо:

1. для устранения подрезания зубьев при z<17 (X>0)

2. для увеличения прочности на изгиб зуба( зуб или основание зуба становится толще), X>0.

3. для получения заданного межосевого расстояния, X>0,X<0.

Положительное смещение X>0 при увеличении прочности зубьев одновременно снижает коэффициент торцевого перекрытия (), а значит увеличивается длительность однопарного зацепления.

Геометрия и кинематика зубчатых передач.

1

П

2

Начальной ( ) называется окружность, проходящая через полис.

Делительной ( ) называется окружность, на которой толщина зуба равняется толщине впадины. Для передач без смещения .

Шагом зацепления ( ) называется расстояние по длине делительной окружности между одноименными точками двух соседних зубьев.

Отношение шага зацепления к  называется модулем зацепления(m).

Это основной параметр от которого зависит величина зуба и зацепление.

Межосевым расстоянием ( ) называется расстояние между осями зубчатых колес.

для внешнего зацепления;

для внутреннего зацепления.

Ширина зубчатого колеса – это длина образующего диска.

диаметр вершин;

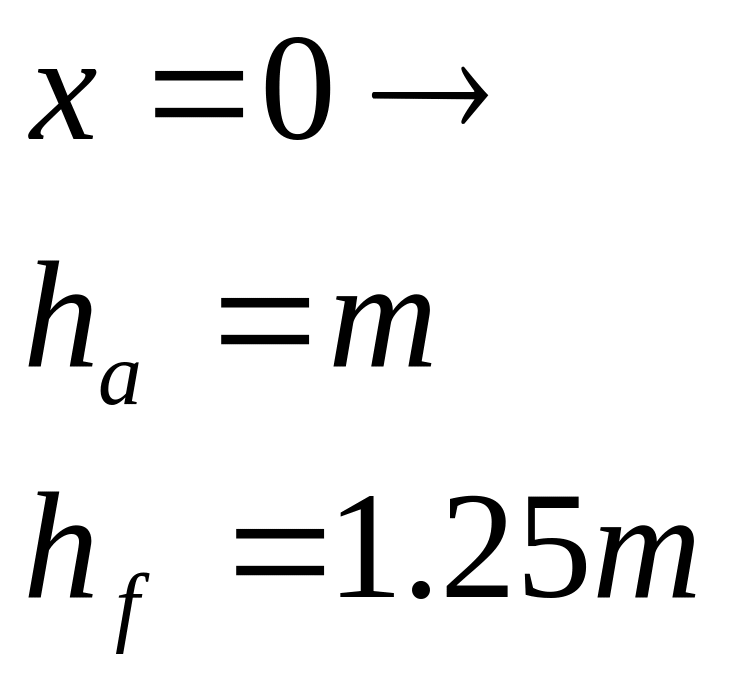
диаметр впадин.

Угол зацепления ( )– угол между перпендикуляром к линии центров и общей нормалью.

Коэффициент торцевого перекрытия ( )определяет число пар зубьев, находящихся одновременно в зацеплении. Для нормальной работы передачи необходимо, чтобы ,т. к. если , то возникает момент, когда в контакте вообще не будет зубьев. Чем больше , тем плавней работает передача.

Например: если , то значит 68% времени зацепления в нем участвует а пары зубьев, а 32% времени - одна пара.

Передаточное число определяется: