83. Свойство транзитивности отношений

отношение R на множестве Х называют транзитивным, если из того, что элемент х находится в отношении R с элементом y, а элемент y находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z: xRy и yRz=>xRz.

Граф транзитивного отношения с каждой парой стрелок, идущих от х к y и от y к z, содержит стрелку, идущую от х к z.Свойством транзитивности обладает и отношение «длиннее» на множестве отрезков: если отрезок а длиннее отрезка b, отрезок b длиннее отрезка с, то отрезок а длиннее отрезка с. Отношение «равенства» на множестве отрезков также обладает свойством транзитивности: (а=b, b=с)=>(а=с).

85.метод квайна-мак-класки для минимизации неполностью определенных .Определение: не полностью определенные ФАЛ от n переменных называется функции, заданные на множестве наборов меньше чем 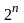.Если количество неопределенных наборов равно m то путем различных доопределений можно получить 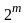различных функций.

87. Свойства операций над множествами.

88. проверка на фиктивность переменных ф-ии. Алгоритм распознавания фиктивной переменной по таблице истинности.1) Для переменной x₁ сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x₁=0, а в нижней x₁=1, если они совпадают, то переменная x₁ фиктивна;2) для переменной x₂ сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x₂ =0, а в нижних x₂ =1, если четвертины в каждой половине совпадают, то переменная x₂ фиктивна;3) и так далее (за четвертинами следуют 1/8, 1/16, … ). Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.

89. произведение отношений. Пусть RAB, SBC. произведение отношений R,S называетс отношение RSAC такое, что aRScbBaRbbSc . Если RAB, SCD и BC, то произведение отношений не определенно.

93. ДНФ- это дизъюнкция элементарных конъюнкций.

94. ДСНФ – это такая ДНФ, которая удовлетворяет условиям:1)в ней нет одинаковых элементарных конъюнкций 2) в каждой конъюнкции нет одинаковых пропозициональных букв 3) каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке. 4) никакая из элемент конъюнкций не содержит перемен вместе с ее отрицанием. Для любой функции алгебры логики существует своя СДНФ, причём единственная.

95. сокращенная ДНФ – дизъюнкция всех простых импликант булевой функции

96. кратчайшая ДНФ – ДНФ имеющая наименьшую длину по сравнению со всеми другими ДНФ. Эквивалентные данной ф-ии называют кратчайший ДНФ.

97. минимальная ДНФ – содержащия наменьшее количество вхождения переменных по сравнению со всеми со всеми другими ДНФ.

98.Метод квайна-Мак-Класки

"Метод представляет собой формализованный на этапе нахождения простых импликант метод Квайна. Формализация производится следующим образом:

1.Все конституанты единицы из СДНФ булевой функции f записываются их двоичными номерами.

2.Все номера разбиваются на непересекающиеся группы. Признак образования i-й группы: i единиц в каждом двоичном номере конституенты единицы.

3.Склеивание производят только между номерами соседних групп. Склеиваемые номера отмечаются каким-либо знаком (зачеркиванием).

4.Склеивания производят всевозможные, как и в методе Квайна. Неотмеченные после склеивания номера являются простыми импликантами.

100. существенные импликанты ФАЛ если в каком либо из столбцов таблицы Квайна имеется только одна метка, то первичная импликанта стоящая в соотвестсвующей строке называется существенной. Существенная импликанта не может быть искл из правой части, так как без нее не будет получено покрытие всего множества данной ф-ии.