35,111.Минимизация фал методом неопределенных коэффициентов

Минимизация ФАЛ. Определение: Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией. Определение: Несклеивающиеся импликанты называются прослойками. Определение: Формула, состоящая из простых импликант – тупиковая. Пример: 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 0 Если в процессе склейки образуется форма R, содержащая члены вида , что позволяет добавить к исходной форме R несколько членов вида пар и после этого продолжить минимизацию. Метод неопределенных коэффициентов. Суть метода состоит в преобразовании ДСНФ в МДНФ. любую ФАЛ можно представить в виде Алгоритм определения коэффициентов: 1. Исходное уравнение разбить на систему уравнений, равных числу строк в таблице истинности. 2. Напротив каждого выражения поставить соответствующее значение функции. 3. Выбрать строку, в которой значение функции к нулю. 4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все коэффициенты, встречающиеся в нулевых строках. 5. Проанализировать оставшиеся коэффициенты в единичных строках. 6. Используя правило, что дизъюнкция равна 1 если хотя бы один из , выбрать mi -термы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно. 7. Записать исходный вид функции. Метод неопределенных коэффициентов применим для дизъюнктивной формы и непригоден для конъюнктивной.

37. количество доопределений неполность определенных ФАЛ. Число различных доопределений неполностью определенной булевой функции f_×(x₁, …, x_n) равно 2^k

38. Таблица истинности эквивалентности и сложение по модулю 2

Логическая равнозначность (эквивалентность, тождество) - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначение: ≡ . 11-1;10-1;01-1;00-0.

Сложение по модулю 2 (исключающее ИЛИ, в просторечье XOR) - определяет результат сравнения двух простых логических выражений А и В. Результатом является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения различны.11-0;10-1;01-1;00-0.

40. свойство транзитивности отношений m_im_jm_k (m_iRm_j)(m_jRm_k) m_i R m_k

41.Предельное разложение шеннона

Предельное разложение Шеннона (k=n) булевой функции f(x₁,x₂,…,x_n), не равной 0, имеет вид:

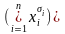Предельное разложение Шеннона булевой функции f(x₁,x₂,…,x_n) является ее СДНФ. В алгебре Буля справедлив принцип двойственности, согласно которому имеем следующие двойственные разложения Шеннона булевой функции f(x₁,x₂,…, x_k , x_k+1,… ,x_n):

По k переменным

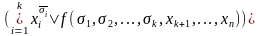
42. нахождение минимального покрытия таблицы Квайна. Покрытием таблицы Квайна -подмножество таких ее строк, которые в совокупности покрывают все столбцы таблицы. Длиной покрытия назовем количество строк, образующих покрытие. Рангом строки таблицы Квайна назовем ранг приписанной ей простой импликанты. Минимальным покрытием таблицы Квайна назовем покрытие с минимальной суммой рангов строк.Нетрудно видеть, что минимальное покрытие таблицы Квайна функции f(x₁, …, x_n) задает минимальную ДНФ_f. Таким образом, задача минимизации булевой функции решается построением таблицы Квайна и поиском минимальных покрытий.

43. найти отношение, обладающее свойствами рефлективности, симметричности, транзитивности. Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойством рефлексивности, симметричности и транзитивности.    Примерами: отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).

46. максимальный интервал ФАЛ. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I', такого что I I'. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

47. не полностью определенные ФАЛ и их минимизация . Подмножество FM_yM_x называется функцией, если для каждого элемента х, х M_x найдется не более одного элемента у M_y вида (х,у)F, при этом ф-ия называется всюду( полностью определенной) , в протвном случае – частично определенной. реально на практике функции либо не определены полностью, либо есть запрещенные комбинации. Минимизировать неполностью определенную булеву функцию – это значит выбрать среди кратчайших ДНФ всех ее доопределений самую короткую ДНФ. Пусть заданна ф-ия f()=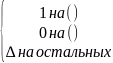 от неполно определенной ф-ии строятся две ф-ии, нулевого определения и единичного доопределения. После этого нахадится лин покрытие конституент един ф-и нулевого определения и ф-ии единичного доопределения. Вместо неопределенностей подставляем 1 решаем методом Квайна-МАК-Класки.