1) 7) .Разложение Шеннона по k переменным Рассмотрим разложение булевой функции f(x₁, x₂,…, x_n) по k переменным (x₁,…, x_k) – разложение Шеннона. Теорема 1. Любая функция f(x₁, x₂,…, x_n), не равная тождественно нулю, представлена в виде разложения Шеннона: За метим, что   если x_i = δ_i, для _i = . Выберем набор δ₁, δ₂,…, δ_k и положим, что x_i = δ_i, i = 1,k. Тогда левая часть будет равна: f(x₁, x₂,…, x_k, x_k+1, …, x_n) = f(δ₁,…, δ_k, x_k+1, …, x_n), а правая: . Здесь   разбиваются на единичные и нулевые наборы. Согласно закону а0 = а, получаем, что левая и правая части формул равны при любой подстановке переменных х₁, х₂,…,х_k.

2. логические ф-ии и логические переменные. Лог. Ф-ией f(x1,x2…xn) называется произвольная н-местная ф-ия, аргументв которой принадлежат множеству {0;1}. Переменные принимающие значение из булева множества называются логическими переменными.

3. Законы де Моргана в алгебре множеств

Законы де Моргана в алгебре множеств формулируются следующим образом:

, если  .

Если   и  , то 

Если  , то для любого   выполняется  . Это соотношение имеет свой аналог в арифметике: если  , то для любого   справедливо  .

4.120 произведение отношений. Пусть RAB, SBC. произведение отношений R,S называетс отношение RSAC такое, что aRScbBaRbbSc . Если RAB, SCD и BC, то произведение отношений не определенно.

5,106 задание отношений фактор-множеством. Фактор множеств- совокупность классов эквивалентности этого множества. Множество окрестностей единичного радиуса, взятых для всех эл-ов мн-ва М при задании в нем отношения R₂M², называется фактором-множеством M/R₂мн-ва М по отношению R_2. Фактор-мн-во M/R₂ полностью оредел отношение R₂.

6,123. Диаграмма Эйлера-венна для иллюстрации операции над множествами

Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже с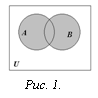 уществующих.

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

 

О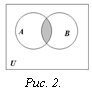 пределение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

 

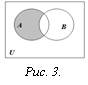
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

 

О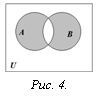 пределение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

8. Таблица истинности функций импликации

Логическое следование (импликация) образуется соединением двух высказы­ваний в одно с помощью оборота речи «если..., то..,».

Логическая операция импликации «если А то В», обозна­чается А ® B и выражается с помощью логической функции F14. которая задается соответствующей таблицей истинно­сти.

Таблица истинности логической функции импликация:00-1;01-1; 01-1;10-0;11-1

9. Свойство симметричности отношений

Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении с элементом y, следует, что  и элемент y находится в отношении R  с элементом х:   xRy=>yRx . вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к х. Верно и обратное: граф, содержащий вместе с каждой стрелкой, идущей от х к у , и стрелку, идущую от у к х, является графом симметричного отношения.

11. декартово произведение мн-тв. Декартовым произведением множеств называют мн-во эл-ов, которые являются всевозможнвми последовательностями, такие что 1 элемент пренадлежит первому мн-ву , второй второму мн-ву, и т.д. мощность декартового произведение равна произведению пощностей сомножетеля. |M₁M₂..M_n|=|M₁||M₂|…|M_n|

13. построение ДСНФ произвольной ФАЛ. Для того чтобы построить СДНФ прозвольной ФАЛ заданной в табл виде, достаточно выделить наборы, на которых ф-ия принимает значения 1, и для каждого из них ввести в СДНФ полную элементарную конъюнкцию, где любая пременная х, присутствует с отрицанием если _i =0, и без отрицания если равна 1. Очевидно, для любой ФАЛ сущствует единственая СДНФ. Данный вид представления называется каноническим.

15. свойство дистрибутивности дизъюнкции относительно конъюнции a v (b & c) == (a v b) & (a v c) - дистрибутивность дизъюнкции относительно конъюнкции

17,102 отношения(определение) отношение – это подмножество декартового произведения множеств. Отношения используют для описания взаимоотношений отдельных составляющих системы для выявления тех или иных св-тв у множеств. Когда говорят о бинарных отношениях , подразумевают отношения между друмя величинами, объектами, высказываний. Говорят элементы а и в находятся а отношении R, если (а,в) R.

18. простые имплеканты и их нахождение. Конъюнкция , соответствующая макс единичному интервалу ф-ии F, называется простой имплекантой этой ф-ии. Результат склеивания соседних или смежных минитермов называется имплекантой, которая представляет собой конъюнкцию число агрументов которой на 1 меньше, чем в исходном минтерме. Склеивание двух смежных имплекант дает имплеканту эквивалентную 4 минтернам . такие имплеканты называют простыми, состоящими из дизъюнкции простых имплекант, называемой сокращенной ДНФ.

19. способы задания множеств. 1) перечислением- пр перечислении множеств его эл-ты принято заключать в фигурные скобки. 2) аналитический .описание св-тв – для задание некоторого множества Х, состоящего из эл-ов, обладающих св-ом А, используют запись Х={х|А(х)} читается « Х множество элементов х таких, что А(х).