22

Росжелдор

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный университет

путей сообщения»

(ФГБОУ ВПО РГУПС)

ЭЛЕКТРОНИКА

Методические указания к лабораторным работам

Ростов-на-Дону

2013

Лабораторная работа 1. RC-цепи в электронных устройстваХ.

Часть I. Исследование свойств rc-цепей

1. Цель работы

Познакомиться с методами моделирования и анализа переходных процессов и частотных характеристик RC–цепей. Получить представление об особенностях амплитудно-частотных (АЧХ) и фазочастотных характеристик (ФЧХ) цепей первого порядка.

2. Общие сведения

2.1. В динамическом режиме работы электрической цепи необходимо учитывать полное сопротивление ее элементов, называемое импедансом.

Отношение сигналов на входе и выходе цепи, зависящих от частоты называется комплексным коэффициентом передачи цепи или передаточной функцией. Передаточная функция цепи состоит из двух основных характеристик.

Функция К() характеризует зависимость модуля коэффициента передачи от частоты и называется амплитудно-частотной характеристикой цепи.

Функция () описывает зависимость сдвига фаз между входным и выходным сигналами и называется фазочастотной характеристикой (ФЧХ) цепи.

Для определения свойств цепи в частотной области необходимо рассчитать значения граничных частот, средней частоты, полосу пропускания АЧХ, коэффициент передачи на средней частоте.

Свойства электрической цепи во временной области описываются переходной характеристикой h(t), под которой понимают зависимость выходной величины от времени при единичном скачке напряжения на входе цепи. При оценке длительности переходных процессов пользуются условным уровнем , отнесенным к амплитуде скачка сигнала.

Р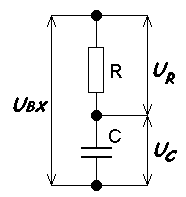 ассмотрим RC-цепь, показанную на рисунке 1, представляющую собой делитель напряжения, коэффициент передачи которого зависит от частоты сигнала. Важным параметром, описывающим свойства цепи во временной области, является постоянная времени цепи , определяющая время, за которое ток в цепи изменится в е раз:  = RC.

Чтобы определить, как изменяется во времени напряжение на выходе RC-цепи при действии на ее входе импульса напряжения прямоугольной формы длительностью tи и амплитудой Um, необходимо воспользоваться вторым законом Кирхгофа U_вх(t) = U_с(t) + U_R(t),

первым законом коммутации i(t)=C du_c(t)/dt

и формулой Ома I=U/R.

Рисунок 1 – RC-цепь

первого порядка

Изменение напряжения на конденсаторе и резисторе происходит по экспоненциальному закону: U_c (0≤ t< tи) = U_m (1-e^-t/) (1)

U_R (0≤ t< tи) = U_m e^-t/ (2)

При построении временных диаграмм и анализе свойств RC-цепей полезно запомнить соотношения напряжений для характерных моментов времени равных , 2,3 и 3, полученные из (1) и (2):

U_C() ≈ 0,63U_m U_R() ≈ 0,37U_m

U_C(2,3) ≈ 0,9U_m (3) U_R(2,3) ≈ 0,1U_m (4)

U_C(3) ≈ 0,95U_m U_R(3) ≈ 0,05U_m

Параметрам цепи во временной области соответствуют параметры частотной области:

_гр= 1/_гр., _гр= 1/2 f_гр.

Свойства электрической цепи зависят от свойств входящих в нее элементов и способов их соединения. Если цепь передает без искажений сигналы в определенной полосе частот и ослабляет сигналы за ее пределами, ее называют фильтром.

Фильтр нижних частот. Рассмотрим RC-цепь, у которой выходное напряжение снимается с конденсатора. В этом случае передаточная функция цепи описывается уравнением первого порядка:

(5)

Для АЧХ и ФЧХ цепи получим:

(6)

() = - arctg   (7)

На определенной частоте сопротивления элементов будут равны, следовательно, будут равны и падения напряжений U_c = U_R. Такую частоту называют частотой полюса _p. Для фильтров первого порядка частота полюса совпадает с граничной частотой _гр. С линейной частотой она связана соотношением:  _гр = 2πF_гр.

Из уравнений (5), (6) и (7) видно, что:

К(0) = 1, К(_гр) = 0,7, К() = 0 ,

(0) = 0^O, (_гр) = - 45^O, () = - 90^O

И з частотных характеристик цепи, приведенных на рисунке 2, видно, что рассмотренная цепь передает без изменения сигналы нижних частот, а на верхних частотах создает затухание выходного сигнала и его задержку по фазе, то есть, является фильтром нижних частот. Его граничная частота называется верхней граничной частотой _в.

Рисунок 2 – АЧХ и ФЧХ фильтра нижних частот

Если входной сигнал представляет собой последовательность прямоугольных импульсов с периодом Т_И = 1/F_И, то форма импульса выходного напряжения будет зависеть от соотношения параметров сигнала и параметров цепи. При  >> t_И (F_В << F_И) выходное напряжение практически линейно зависит от времени. В этом случае ФНЧ называется интегрирующей цепью (рисунок 4а).

Фильтр верхних частот. В случае если выходное напряжение RC-цепи снимается с резистора, передаточная функция цепи описывается уравнением:

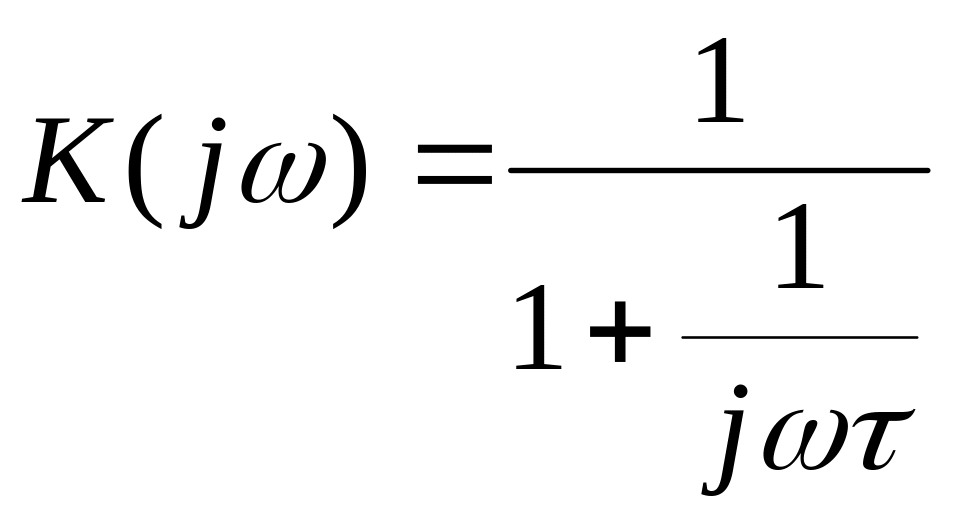(8)

Для АЧХ и ФЧХ цепи получим:

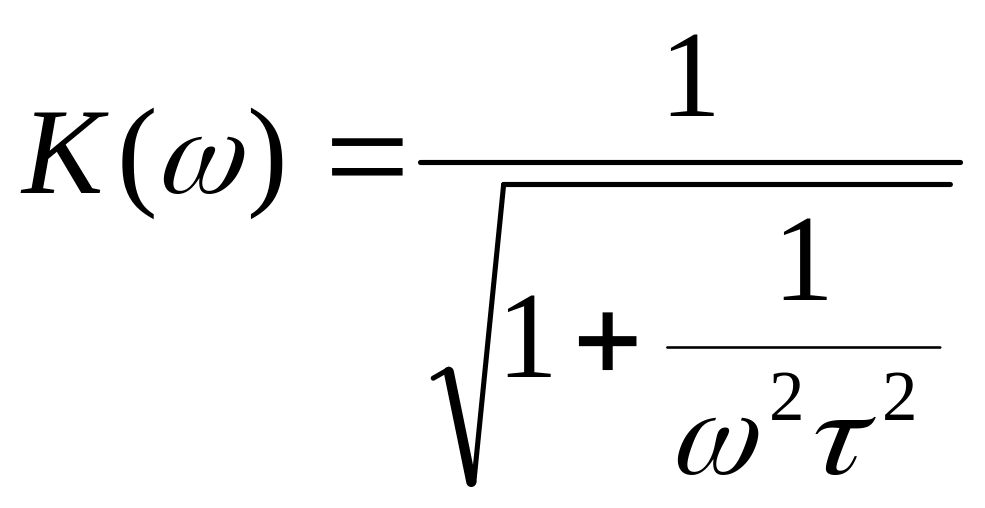(9)

() = arctg 1/  (10)

И з частотных характеристик цепи, приведенных на рисунке 3, видно, что рассмотренная цепь передает без изменения сигналы верхних частот, а на нижних частотах создает затухание выходного сигнала и его опережение по фазе относительно входного. Граничная частота такого фильтра называется верхней граничной частотой _н.

Рисунок 3 – АЧХ и ФЧХ фильтра верхних частот

Входная и выходная цепь ФВЧ разделены конденсатором, через который не может протекать постоянный ток. Поэтому постоянная составляющая входного напряжения в выходную цепь не передается. На этом основано применение фильтра в качестве разделительной цепи связи между каскадами электронных устройств.

При подаче на вход ФВЧ прямоугольных импульсов с t_И <<  (F_И >>F_Н) формы входного и выходного импульсов практически совпадут. При  < t_И ФВЧ укорачивает длительность выходного импульса. Такую цепь называют укорачивающей (рисунок 4 б).

Если  << t_И (F_Н >> F_И), напряжение на выходе не равно нулю только в течение короткого времени после скачка входного напряжения. Такой фильтр ведет себя аналогично дифференцирующей цепи (рисунок 4 в).

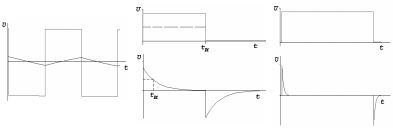
а) б) в)

Рисунок 4 – Временные диаграммы выходных сигналов RC-цепей

При построении частотных и временных характеристик цепей, с учетом дополнительно подключенных элементов, или при учете влияния сопротивлений генератора и нагрузки, необходимо производить перерасчет значений постоянной времени цепи, граничных частот и коэффициента передачи.

Соединяя последовательно фильтры верхних и нижних частот, можно получить электрические цепи, передающие практически без искажений сигналы в определенной полосе частот и подавляющие сигналы за ее пределами. При условии, что граничная частота ФВЧ не превышает граничную частоту ФНЧ, в результате такого соединения получится двухзвенный полосовой фильтр второго порядка. АЧХ и ФЧХ такого фильтра представлены на рисунке 5.

Рисунок 5 – АЧХ И ФЧХ полосового фильтра