7. Квантовая гипотеза Планка

Теоретическое объяснение законов теплового излучения абсолютно чёрного тела имело огромное значение в истории физики - оно привело к понятию квантов энергии. С классической точки зрения вывод формулы Релея – Джинса является безупречным. Поэтому расхождения этой формулы с экспериментом указывало на существование каких – то закономерностей несовместимых с представлением классической физики. В 1900 году Планку удалось найти вид функции в точности соответствующей экспериментальным данным.

Макс Планк предположил, что теория классического гармонического осциллятора неприменима к атомным осцилляторам; атомные осцилляторы излучают энергию не непрерывно, а определёнными порциями — квантами. Энергия одного кванта:

(7.1)

где = 6,626∙20^-34 Дж∙с - постоянная Планка, - нормированная постоянная Планка, - циклическая частота.

В механике есть имеющая размерность "энергия × время" величина, которая называется действием. Поэтому, постоянную Планка иногда называют квантом действия. Размерность совпадает с размерностью момента импульса.

Поскольку энергия излучается порциями, то энергия осциллятора может принимать лишь определённые дискретные значения, кратные целому числу квантов:

(7.2)

где - число квантов. Среднюю энергию осцилляторов нельзя принимать равной , как это делал Джинс, поскольку это приводит к "ультрафиолетовой катастрофе".

В состоянии равновесия распределение колебаний по значениям энергии должно подчиняться распределению Больцмана. Это распределение показывает, что энергии осцилляторов располагаются на шкале энергии с большей плотность там, где их энергия меньше. Вероятность , того, что энергия колебания осциллятора частоты имеет значение , определяется выражением (1.13):

(7.3)

где - число осцилляторов с энергией ; - полное число осцилляторов. Если в полости, представляющей собой модель абсолютно чёрного тела, имеется осцилляторов, то среднее значение энергии излучения с частотой , приходящейся на один осциллятор

Вычисления дают выражение для средней энергии осцилляторов:

(7.4)

Следует заметить, что при , формула переходит в классическое выражение .

Подставив (7.4) в формулу полученную Джинсом (6.7) Планк получил универсальную функцию Кирхгофа в виде,

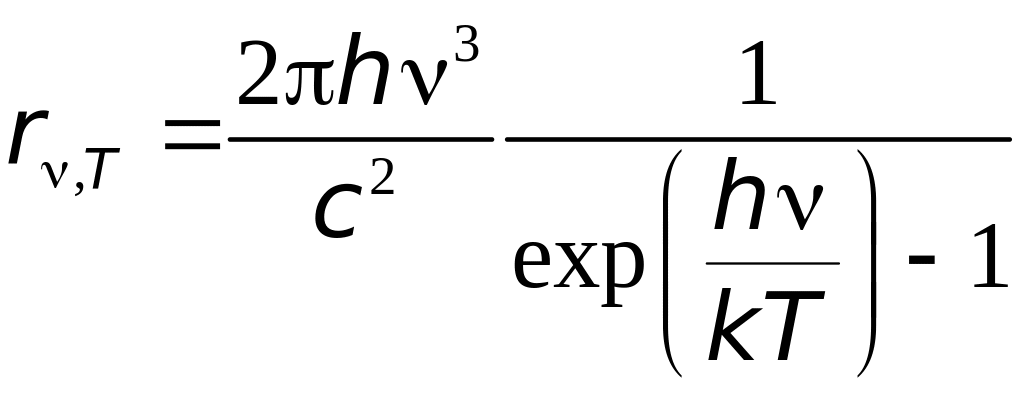(7.5)

Или в виде - функции длины волны (учитывая , ).

(7.6)

Формула в виде (7.5) или в виде (7.6) носит название — формулы Планка.

В области малых частот << (когда энергия кванта мала по сравнения с энергией теплового движения ) формула Планка (7.5) переходит в формулу Рэлея-Джинса (6.7). Для доказательства разложим экспоненту в знаменателе (7.5) в ряд Маклорена, ограничиваясь двумя первыми членами:

,

тогда и в знаменателе (7.5) остаётся только . Сократив , получим формулу Релея–Джинса:

.

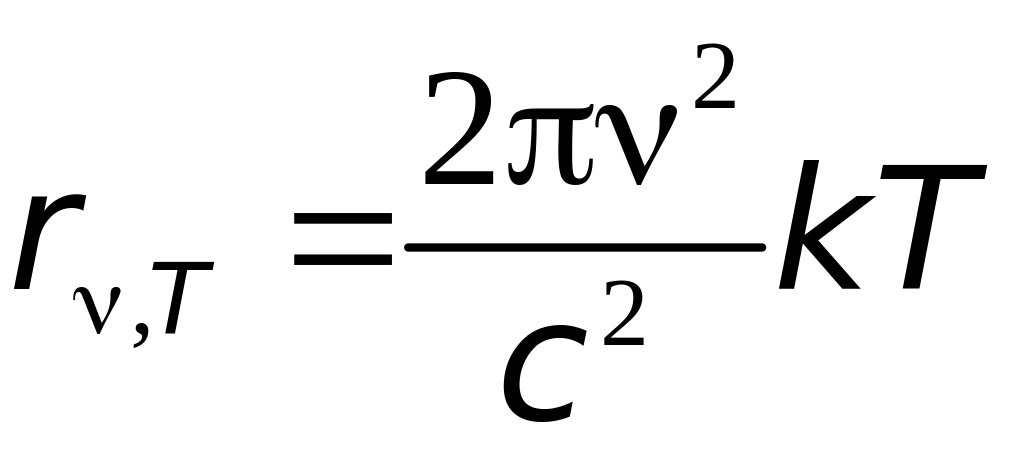Закон Стефана-Больцмана получается из формулы Планка её интегрированием по частотам.

.

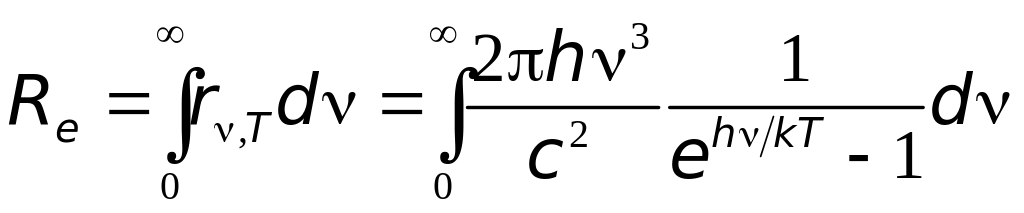Ведём безразмерную переменную . Тогда а . Подставим выражения для и под интеграл, вынесем из - под знака интеграла комбинации постоянных и в результате получим:

(7.7)

где

- постоянная Стефана-Больцмана. Осталось взять интеграл, который равен:

.

Таким образом, теоретическое значение постоянной Стефана–Больцмана можно рассчитать по формуле:

. (7.8)

Что самое удивительное этот расчёт даёт значение постоянной Стефана-Больцмана совпадающее с экспериментальным значением = 5,7∙10^-8 Вт/(м² К⁴).

Закон смещения Вина получается при анализе формулы Планка (7.6) на экстремум. Для этого возьмём производную от правой части формулы (7.6) и приравняем её нулю.

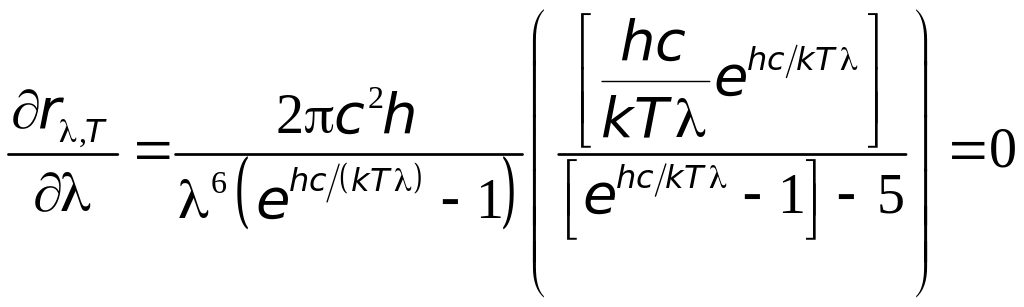
Введя обозначение , получим уравнение:

Решение этого трансцентдентного уравнения методом последовательных приближений даёт . Следовательно , откуда:

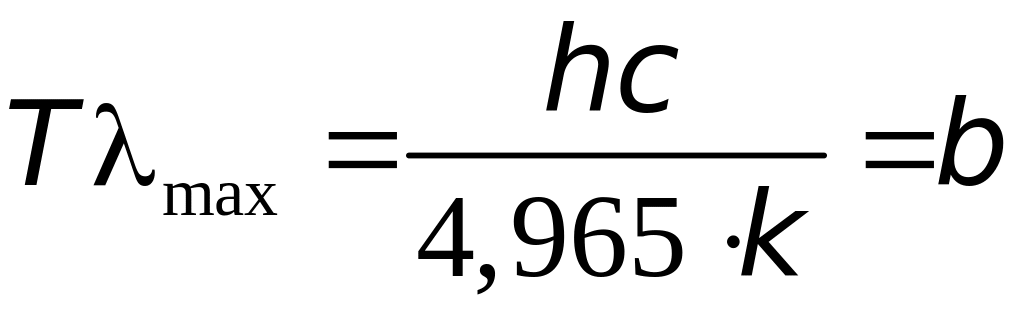(7.9)

Таким образом, формула Планка обобщает все законы теплового излучения и является полным решением основной задачи теории теплового излучения.