30. Теор. О виде реш. Ур. Лоду-2п-пк
1.Если
число
-
вещественный корень уравнения
алгебраической уравнении:

То
функция
 является решением уравнения ЛОДУ-2п-пк.
является решением уравнения ЛОДУ-2п-пк.
2.
Если число
 и
и
 – комплексные корни уравнении
где
– комплексные корни уравнении
где
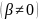
 то
то
функция
 и
и
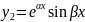 , являются решением уравнения ЛОДУ-2п-пк.
, являются решением уравнения ЛОДУ-2п-пк.
31. Теор. О струк. Общ. Реш. Лоду-2п-пк
Уравнение
вида:
 называется общим решением ЛОДУ-2п-пк .
называется общим решением ЛОДУ-2п-пк .
1.
Если корни его характеристического
уравнения :
, вещественные и различные:
 то общее решение ЛОДУ-2п-пк имеет вид:
то общее решение ЛОДУ-2п-пк имеет вид:
 ,
,

2.
Если корни его характеристического
уравнения вещественные и равные:
 то
общее решение ЛОДУ-2п-пк имеет вид
то
общее решение ЛОДУ-2п-пк имеет вид
 ,
,

3.
Если корни его характеристического
уравнения комплексные:
и
,
, то общее решение ЛОДУ-2п-пк имеет вид
:

32. Теор. О наложении решений лнду-2п-пк
Если
 -решение
ЛНДУ-2п-пк:
-решение
ЛНДУ-2п-пк:

а
 -
решение ЛНДУ-2п-пк:
-
решение ЛНДУ-2п-пк:
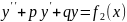 , то сумма
+
-
является решением ЛНДУ 2п-пк:
, то сумма
+
-
является решением ЛНДУ 2п-пк:

(Дополнительная
информация)
Есть
4 типа ЛНДУ 2п-пк:
1.
2.
3.
4.



 является решением уравнения ЛОДУ-2п-пк.
является решением уравнения ЛОДУ-2п-пк. и
и
 – комплексные корни уравнении
где
– комплексные корни уравнении
где
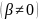
 то
то и
и
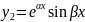 , являются решением уравнения ЛОДУ-2п-пк.
, являются решением уравнения ЛОДУ-2п-пк. называется общим решением ЛОДУ-2п-пк .
называется общим решением ЛОДУ-2п-пк . то общее решение ЛОДУ-2п-пк имеет вид:
то общее решение ЛОДУ-2п-пк имеет вид:
 ,
,

 то
общее решение ЛОДУ-2п-пк имеет вид
то
общее решение ЛОДУ-2п-пк имеет вид
 ,
,


 -решение
ЛНДУ-2п-пк:
-решение
ЛНДУ-2п-пк:

 -
решение ЛНДУ-2п-пк:
-
решение ЛНДУ-2п-пк:
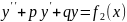 , то сумма
+
-
является решением ЛНДУ 2п-пк:
, то сумма
+
-
является решением ЛНДУ 2п-пк:




