Ответы по коллоквиуму «Дифференциальные уравнения»

1.Опр. дифф-ного ур.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную, её функцию и производные (дифференциалы) этой функции:

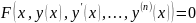
В этом уравнении -независимая переменная, -искомая функция, -производные искомой функции.

2.Опр. порядка дифф-ного ур.

Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.

3.Опр. дифф-ного ур. 1-п

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную , искомую функцию и её производную :

4.Опр. решение дифф-ного ур. 1-п

Решением дифференциального уравнения 1-п называется такая дифференцируемая функция, которая при подстановке в уравнение обращает его в тождество.

5.Опр. начального условия для дифф-ного ур. 1-п

Условие , в силу которого функция 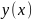принимает заданное значение в заданной точке , называют начальным условием для дифференциального уравнения 1-п

6.Опр. общ. Решения дифф-ного ур 1-п

Общим решением дифференциального уравнения 1-п называется функция: 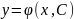, зависящая от и одной произвольной постоянной , если она обладает следующими свойствами:

1.функция является решением данного уравнения при каждом фиксированном значении произвольной постоянной ;

2.для любого начального условия существует единственное значение постоянной , при котором решение удовлетворяет заданному начальному условию.

7. Опр. Частного Решения дифф-ного ур 1-п

Частным решением дифференциального уравнения 1-п называется любая функция:

Полученная из общего решения при конкретном значении постоянной .

8.Опр. Задачи Коши

Задача, в которой требуется найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию, называется задачей Коши.

9. Опр. Дифф-ного ур. 1-п с раздел. Пер.

Уравнения вида: , где - непрерывные функции, называются дифференциальным уравнением 1-п с разделяющимися переменными.

Перед и стоят произведения двух функций, одна из которых зависит от , другая – от , причем некоторые из них могут быть равны константам.

Метод решения:

Перед не должно быть функции, зависящей от . Перед не должно быть функции, зависящей от . Поэтому делим обе части уравнения на функции и :

Одно слагаемое содержит только переменную , другое слагаемое – только переменную . Интегрируем, получаем общий интеграл уравнения:

(Дополнительная информация)

Уравнение вида: , где и - однородные функции одинакового порядка. Её можно записать в виде: , где в левой части стоит производная искомой функции, а в правой – функция, в которой и присуствуют только в виде отношения .

Метод решения:

Вводим новую искомую функцию . Тогда . Вычисляем