Решение игр в частных случаях

В силу антагонистичности особую роль в матричных играх играет понятие доминирования.

Для первого игрока:

Если при сравнении двух некоторых строк матрицы оказывается, что элементы первой меньше либо равны соответствующих элементов второй строки, то это означает, что первая строка доминируется второй строкой (это можно сказать о соответствующих ходах).

Ясно, что для этой игры (при любом поведении соперника) доминируемые ходы не следует выбирать и их можно исключить (соответствующую строку вычеркнуть из матрицы ). А в случае наличия доминирующей строки первый игрок всегда должен выбирать такой ход.

Для второго игрока:

Если в матрице имеется два столбца такие, что элементы первого больше либо равны соответствующих элементов второго столбца, то ему ни при каком поведении соперника нет смысла выбирать первый столбец. И этот столбец называется доминируемым (вместе с ходом) и может быть исключен (вычеркнут) из матрицы .

После исключения доминируемых ходов первого и второго игроков получаем матрицу выигрышей эквивалентную исходной, а в смешанных стратегиях доминируемых ходов первого и второго игроков соответственно , , т.е. доминируемые ходы игроков пассивны.

Пример 3.1.5. Пусть задана матрица игры. Найти цену игры.

Найдем .

Ход доминируется (вычеркиваем ). Ход доминируется (вычеркиваем ). и не доминируют друг друга. Ходы доминируются (вычёркиваем ).

В результате упрощения получаем игру эквивалентную исходной:

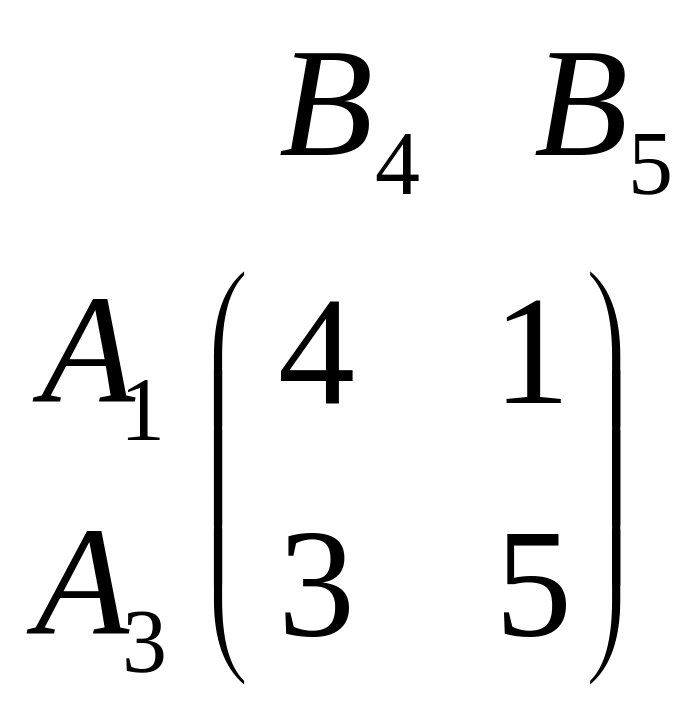
В оптимальной смешанной стратегии первого игрока : ; второго игрока : . Соответствующие ходы будут всегда пассивны.

Решение игр . Геометрическая интерпретация

Справедлива следующая теорема:

Теорема: пусть первый игрок выбирает - оптимальную смешанную стратегию, тогда его средний выигрыш все равно будет , если другой игрок выбирает любую смешанную стратегию, не выходящую лишь за пределы активных ходов из . Аналогичное утверждение справедливо для второго игрока.

Замечание. Если ко всем элементам матрицы некоторой игры прибавить одну и ту же константу , то это не окажет никакого влияния на оптимальные смешанные стратегии первого и второго игроков, лишь цена новой игры будет равна . Поэтому будем считать, что . Тогда и , i= , j= .

Такие две игры будут эквивалентными.

Пусть и задана матрица игры.

(3.1.6)

Пусть в этой игре нет седловой точки, т.е. , тогда очевидно, что оба хода и для первого и для второго игроков будут активными.

Пусть первый игрок придерживается своей стратегии , а второй игрок постоянно выбирает чистый ход . Тогда по теореме получаем

(3.1.7)

Если второй игрок все время выбирает , то

(3.1.8)

Добавляя сюда условие

(3.1.9)

получаем систему

т.е. нахождение оптимальной смешанной стратегии первого игрока и цены задачи сводится к системе (3.1.7), (3.1.8), (3.1.9).

Пусть второй игрок придерживается .

Тогда, если первый игрок выбирает , то его средний проигрыш будет определяться формулой,

(3.1.10)

Если же первый игрок придерживается хода ( постоянно), то

(31.11)

и

(3.1.12)

Получаем систему

(3.1.3)

Таким образом, для решения матричной игры достаточно составить две системы (3.1.7) – (3.1.9), (3.1.10) – (3.1.12) и их решить.

Замечание. При решении этих двух систем, если вначале решить (3.1.7) – (3.1.8) – (3.1.9) и найти цену игры , то можно подставить в (3.1.10) – (3.1.11) – (3.1.12) и останется система с двумя неизвестными. При таком решении либо формулу (3.1.10) либо формулу (3.1.11) можно исключить.

Пример 3.1.6. Пусть игра задана матрицей:

Составим систему уравнений для первого игрока:

Решением игры будет: , , .

Составим систему уравнений для второго игрока:

Решением игры будет: , .

Геометрическая интерпретация

Для первого игрока: Строим систему координат . По оси O откладываем выигрыш игрока; на отрезке [0,1] по оси Op – его смешанную стратегию.

Ось ординат соответствуют выбору хода . Прямая p=1 соответствует ходу .

Если второй игрок выбирает свой ход , то выигрыш первого игрока определяется отрезком [5, 2].

Если же второй игрок выбирает , то выигрыш первого игрока определяется отрезком [–1, 4].

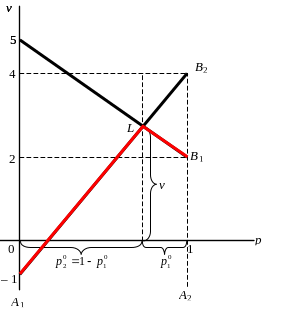
Рис. 3.1.1

Пусть на каждую смешанную стратегию первого игрока второй игрок отвечает наихудшим образом. Тогда выигрыш первого игрока будет определяться нижней ломаной.

Естественно, чтобы в такой ситуации первый игрок выиграл наибольшую величину, он должен подобрать смешанную стратегию, соответствующую высшей точке этой ломаной - . Абсцисса этой точки определяет оптимальную смешанную стратегию первого игрока, а ордината есть не что иное как цена игры. Это и есть решение системы (3.1.7) – (3.1.8) – (3.1.9).

Для второго игрока:

Строим систему координат . На O откладываем выигрыш игрока, на [0,1] – смешанную стратегию.

Ось ординат соответствует ходу . Прямая q=1 – ходу .

Если первый игрок выбирает ход , то выигрыш второго определяется отрезком [5,-1]; если первый игрок выбирает , то у второго игрока выигрыш на [2,4].

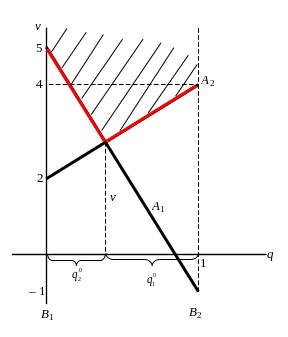
Рис. 3.1.2

Пусть на каждую смешанную стратегию второго игрока первый игрок отвечает наихудшим для него образом.

Тогда при таком поведении первого игрока проигрыш второго определяется верхней ломаной, а наилучшая смешанная стратегия второго игрока будет соответственно нижней точке этой ломаной. Абсцисса точки задает оптимальную смешанную стратегию второго игрока, а ордината – цену игры. Это и есть решение системы (3.1.10) – (3.1.11) – (3.1.12).

Возможны случаи:

, Cедловая точка-

, седловые точки

Рис.3.1.3 Рис.3.1.4

Геометрическая интерпретация и решение игр и

Пусть игра представлена матрицей А¹ или А²:

(3.1.14)

(3.1.15)

Используя результаты предыдущего пункта, решение этих игр можно свести к решению двух систем из трех уравнений с тремя неизвестными. Перед тем как составить эти системы нужно решить геометрически эти игры.

Пример 3.1.7. а) случай .

Пусть игра задана следующей матрицей:

В системе координат строим отрезки [2,1]; [1,3]; [5,4]; [3,0].

Рис. 3.1.5

Затем строим нижнюю ломаную (это линия наихудшего ответа второго игрока на каждую смешанную стратегию первого), определяем её высшую точку .(см. Рис.3.1.5). По этому графику приближенно можно посчитать - оптимальную смешанную стратегию первого игрока и цену игры . Для нахождения их точного значения определяем, что в точке пересекаются и (соответствующие ходы второго игрока будут активными в ). Следовательно, исходная игра эквивалентна игре .

По этой матрице составляем алгебраические системы (игра )

Ответ: ; = 1 ; .

Общая схема решения игры

1. вводим систему координат и проводим линию

2. для каждого хода строим соответствующий отрезок, j=

3. строим нижнюю ломаную из кусков

4. находим верхнюю точку этой нижней ломаной и определяем какие ходы второго игрока будут активными в игре (пересекаются в этой точке)

5. строим эквивалентную игру и две алгебраические системы для нахождения оптимальных стратегии ( для пассивных ходов).

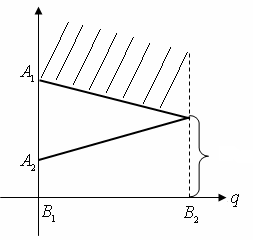
Пример 3.1.8.б) случай , пусть задана матрица:
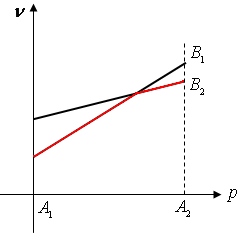