Панель, выполненная из различных материалов

Допустим, что панель на (рис. 32) выполнена из различных материалов. При сжатии или растяжении такой конструкции деформации «ε» всех продольных элементов будут равны, но даже при самых незначительных нагружениях, напряжения в элементах из разных материалов будут различны.

Действительно:

А , следовательно ,

Откуда .

Расчет на изгиб. Метод редукционных коэффициентов.

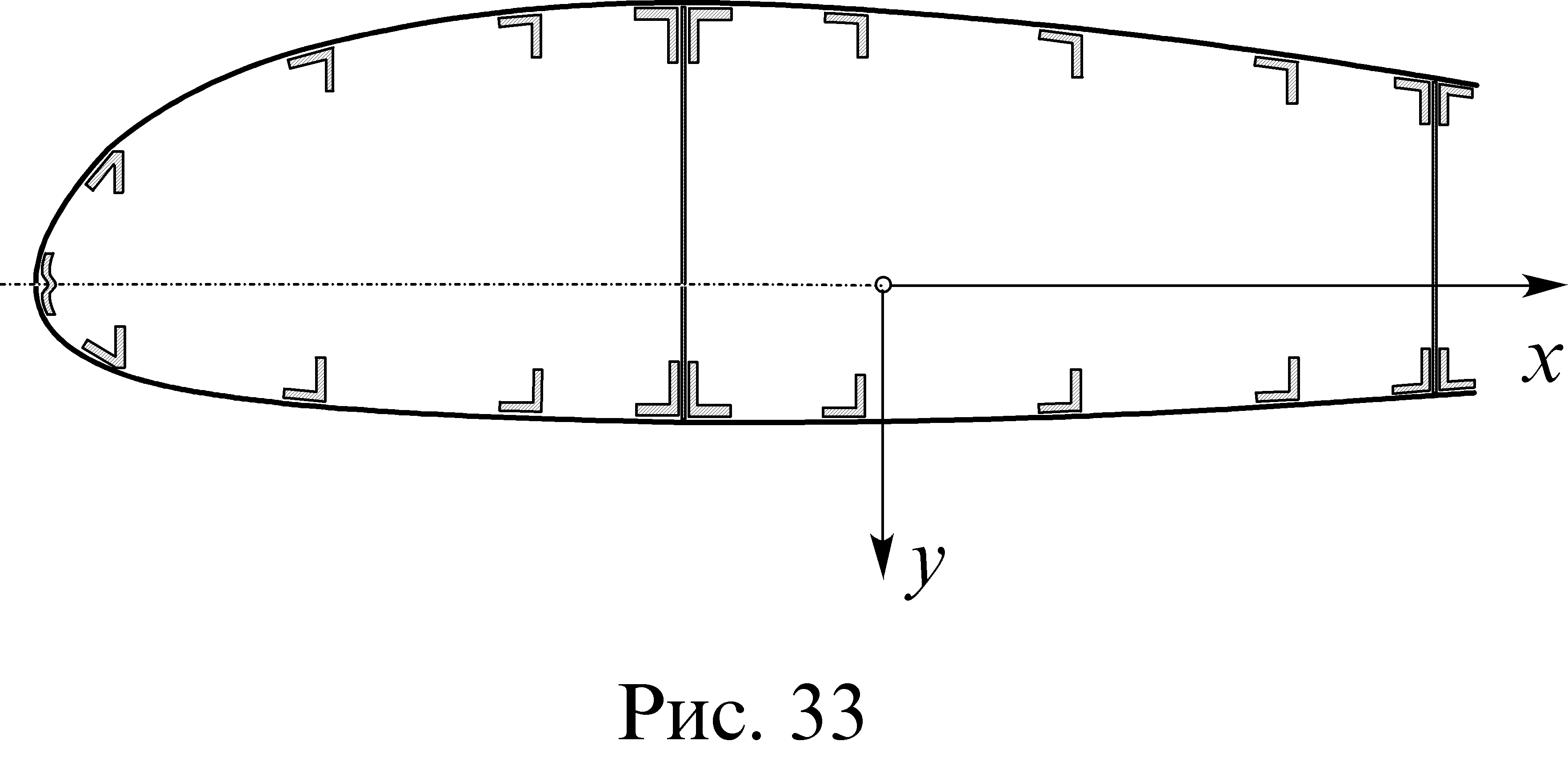
Пусть цилиндрическое тонкостенное крыло, одно из сечений которого изображено на (рис. 33), изгибается в плоскости yOz моментом М_х. такое крыло воспринимает нагрузку как единая пустотелая балка и в сечении образуется общая нейтральная ось, являющаяся вынужденной осью по отношению к любому из элементов сечения.

В этом случае панели крыла будут работать на сжатие и растяжение, как было установлено в предыдущих лекциях. Продольные ребра (стрингеры, полки лонжеронов) с присоединенной обшивкой будут представлять их сосредоточенными в точке, совпадающей с их центром тяжести. Координаты центров тяжести этих элементов обозначим x_i и y_i.

Нормальные напряжения σ_i, возникающие в результате изгиба крыла в каждом из элементов сечения, должны, очевидно, удовлетворять уравнениям равновесия:

Сумма проекций внутренних сил на ось Z:

Сумма моментов внутренних сил относительно оси Y

Сумма моментов внутренних сил относительно оси X

Распишем эти уравнения:

; ; (2.9)

Умножим каждый член этих сумм на множитель и вынесем за знак сумм

Здесь – искомое нормальное напряжение в растянутой полке наиболее мощного лонжерона, – ордината центра тяжести лонжерона в выбранных, но пока неизвестных осях.

Тогда уравнение (2.9) можно записать так:

; ;

Сокращая первые два уравнения на и обозначая безразмерный, всегда положительный коэффициент , (2.10)

Получим систему из трех уравнений относительно большого числа неизвестных σ_i:

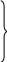(2.11)

Разрешить эту систему невозможно без введения дополнительных кинематических допущений.

Предположим:

1. при изгибе деформации распределяются по сечению, подчиняясь закону плоскости

2. модули упругости всех элементов сечения, работающих на нормальные напряжения, одинаковы (E_i = E)

3. во всех элементах деформации не выходят за пределы применимости закона Гука, т.е. , и ни один из них не теряет устойчивости.

Тогда, подставляя значение ε_i, получим , т.е. напряжения распределяются по закону плоскости.

В этом случае введенный нами коэффициент (2.10) обратится в единицу:

,

Следовательно, уравнения (2.11) примут вид:

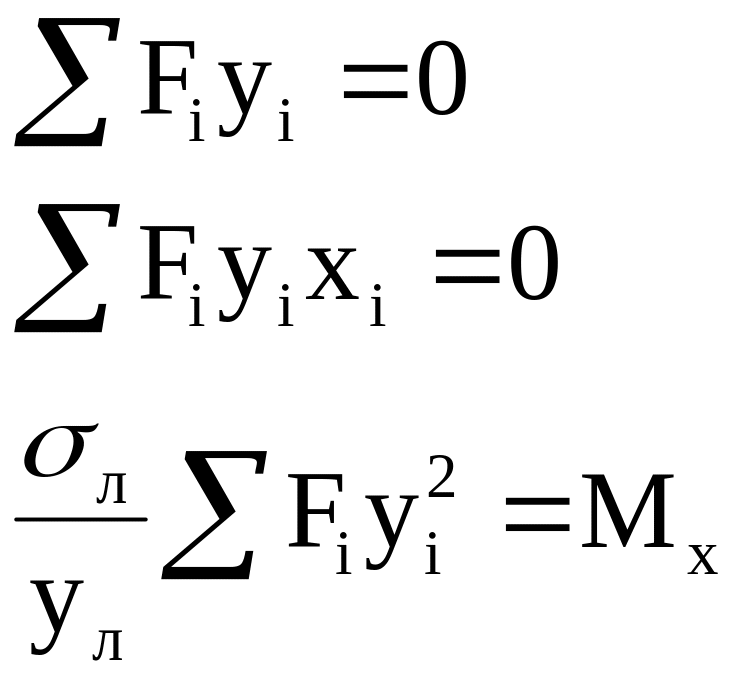
Но – статический момент площадей сечения относительно оси Х

– центробежный момент,

– момент инерции сечения относительно оси Х.

Следовательно, разрешающими уравнениями в данном случае будут:

(2.12)

Т.к. , то (2.13)

Таким образом, мы получили элементарные разрешающие уравнения для изгиба балки относительно одной из главных осей, рассматриваемых в сопротивлении материалов.

В тонкостенных конструкциях, как видно на примере панелей, последнее (третье) предположение имеет место только при очень незначительном нагружении. При нагрузках же, которые являются расчетными для крыла, большинство элементов сжатой зоны конструкции обычно теряет устойчивость и, следовательно, их сопротивление деформации в основном направлении уже не подчиняется закону Гука. Кроме того, элементы конструкции могут иметь различные модули упругости. Т.о., высказанные ранее предположения 2 и 3 не соответствуют физическому явлению, наблюдаемому при изгибе тонкостенного крыла, потому формулы (2.12) и (2.13) не могут быть использованы.

Очевидно, что в общем случае φ_i не будет равно единице, и для расчета нам придется пользоваться уравнениями (2.11)

Введем обозначение (2.14)

Будем называть такую площадь приведенной или редуцированной площадью, а φ_i – редукционным коэффициентом.

Тогда уравнения (2.11) перепишутся так:

(2.15)

Однако

Т огда (2.16)

Видно, что уравнения (2.16) такие же как уравнения (2.12) сопротивления материалов. Разница в том, что в уравнениях (2.16) вместо действительных площадей сечения конструкции вошли приведенные редуцированные площади.

Если бы мы знали эти приведенные площади или редукционные коэффициенты φ_i, мы легко разрешили бы уравнения (2.16) и знали бы σ_л, а далее и напряжения в любом элементе сечения, т.к. , откуда , или после подстановки из последней формулы (2.16) получим

(2.17)

Полученный результат можно сформулировать следующим образом: в общем случае тонкостенную конструкцию можно рассчитать с помощью элементарных формул сопротивления материалов, но при расчете принимать во внимание не полные площади элементов сечения, а редуцированные, причем редукционный коэффициент .

Но редукционный коэффициент сам является функцией неизвестных искомых величин , т.к. не только напряжения, но и нейтральная ось изгиба до расчета не известны.

Поэтому приходится прибегать к методу последовательных приближений.

1. Будем предполагать, что сопротивление сжатию элемента, потерявшего устойчивость, не зависит от деформации (сплошная линия на рис. 34)

2. Снижение напряжений в тонкостенных элементах, имеющих место при растяжении, помимо явления текучести, будем относить за счет модулей упругости E_i.

3. Диаграммы растяжения с эффектом упрочнения будем заменять двумя прямыми (рис.35), предполагая материал идеально пластичным.

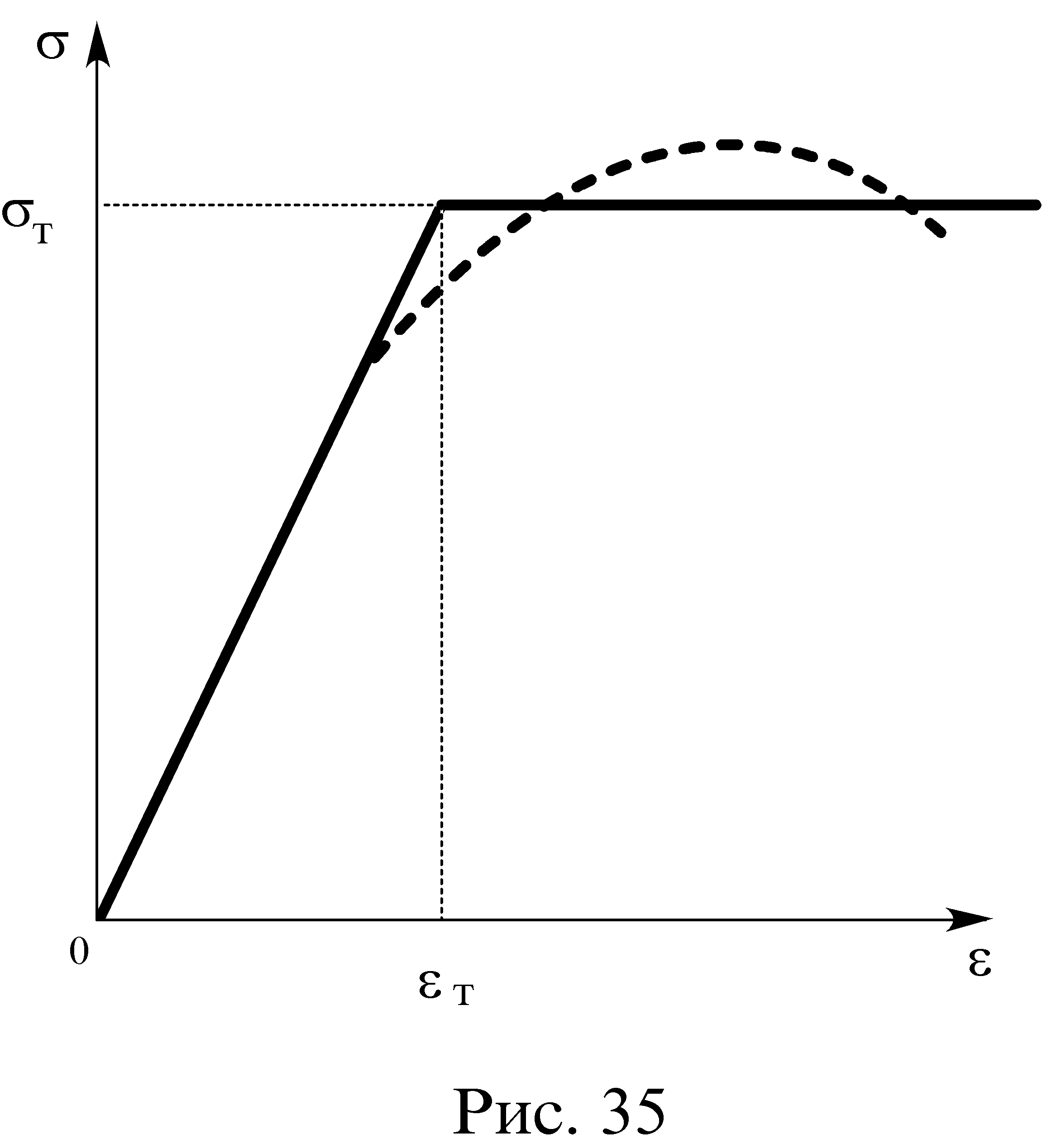
Тогда напряжения в любом элементе, в зависимости от его деформации, можно записать так:

(2.18)

Где η_i – некоторый множитель.

Если обозначить ту деформацию, при которой диаграмма σ – ε имеет излом ( – при сжатии, – при растяжении), то множитель η_i будет таков:

При ,

При ,

Используя (2.18), запишем редукционный коэффициент:

(2.19)

Здесь мы приняли , т.к. в основном лонжероне напряжения не должны превосходить σ_т.

Рассмотрим формулу (2.19) подробнее

1. Допустим, что в каком-то элементе абсолютное значение деформации при сжатии меньше , или при растяжении меньше , тогда , и .

Но т.к. нами принята гипотеза плоского распределения деформаций ( ), редукционный коэффициент для таких элементов конструкции будет равен:

(2.20)

В том случае, когда модули упругости элемента и лонжерона одинаковые, .

2. Если какой-либо сжатый элемент имеет абсолютную деформацию больше , или растянутый элемент больше, чем , то соответствующие редукционные коэффициенты будут равны:

;

Переходя к напряжениям, получим:

; (2.21)