Нагружение самолета. Нагрузки самолета. Нормы прочности.

Для расчета самолета на прочность, прежде всего, необходимо знание действующих на него нагрузок. Однако нагрузки, действующие на агрегаты самолета, непостоянны во времени. Они изменяются в зависимости от режима и условий полета. При этом изменяется не только величина сил, но и их направление, и характер распределения по поверхности агрегата.

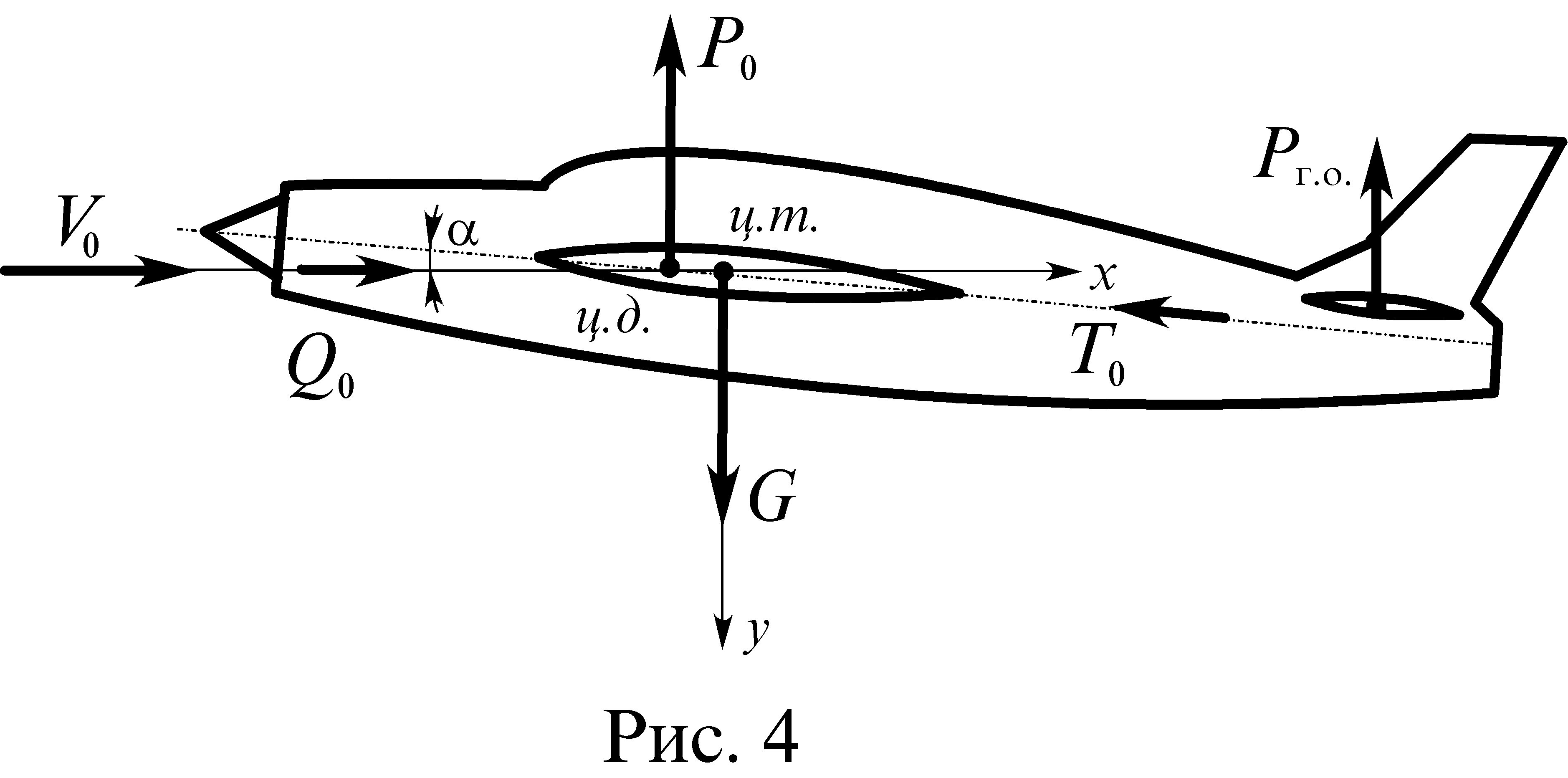
В равномерном горизонтальном полете силы, действующие на самолет, находятся в равновесии:

1. Подъемная сила крыла Р₀, распределенная по его поверхности. Равнодействующая этой нагрузки приложена в центре давления (рис. 4)

2. Подъемная сила горизонтального оперения Р_г.о., уравновешивающая момент сил относительно оси Z, проходящей через центр тяжести самолета.

3. Сила тяги двигателя Т₀.

4. Сила лобового сопротивления Q₀.

5. Вес самолета G.

Однако, нагрузки на горизонтальное оперение Р_г.о малы по сравнению с подъемной силой крыла, поэтому для упрощения анализа ими можно пренебречь. Одновременно будем полагать, что равнодействующие аэродинамических сил и тяги двигателей, проходят через центр тяжести самолета, а тяга двигателей, кроме того параллельна вектору скорости V₀ (рис. 5).

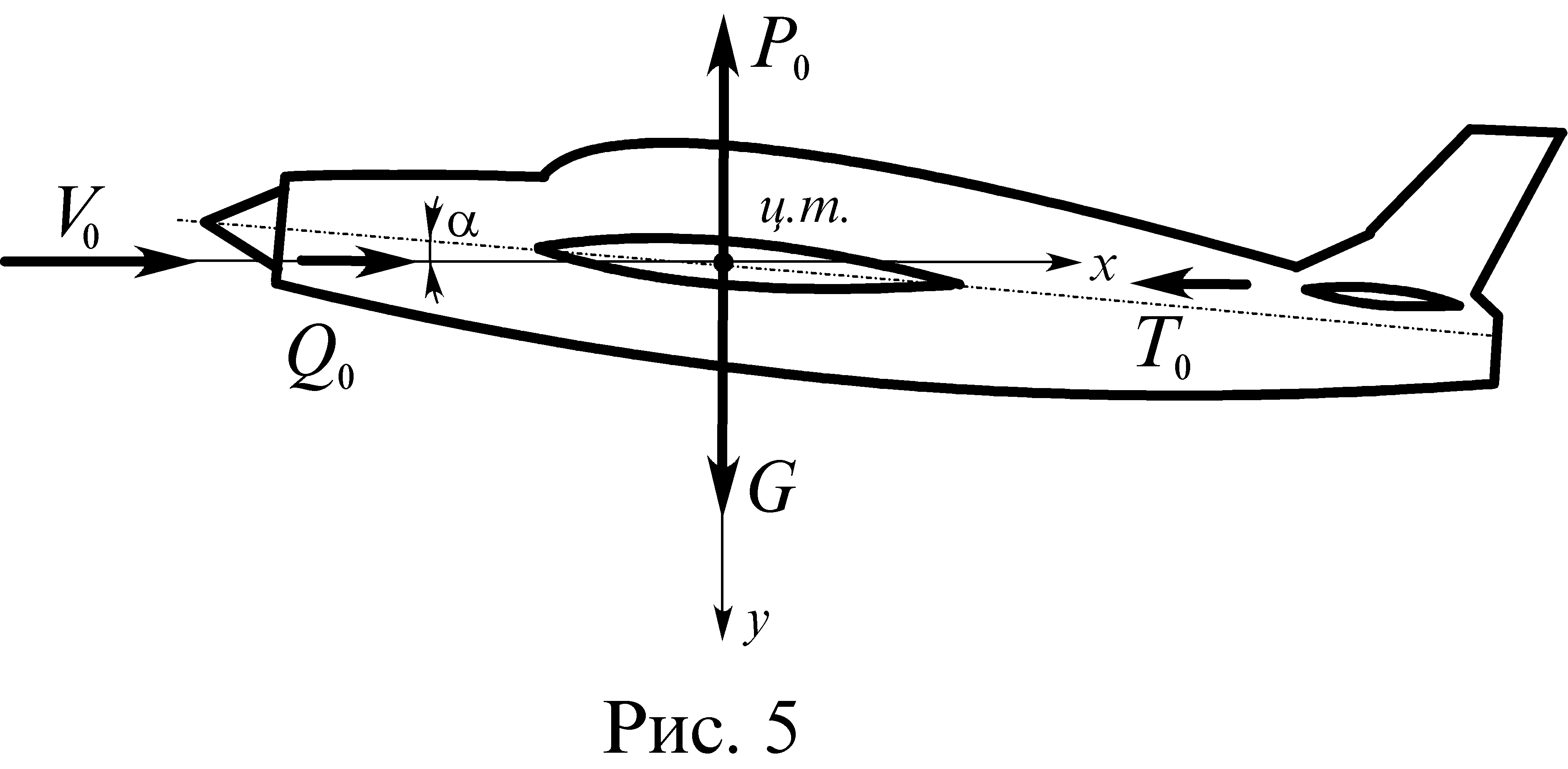
Из условия равновесия: Р_о = G ; Q_o = T_o (1.1)

т.е. в равномерном горизонтальном полете подъемная сила крыла равна весу самолета.

В условиях неравномерного криволинейного полета в общем случае ни равновесие сил, ни равновесие моментов, действующих на самолет, уже не будет. Неуравновешенные составляющие сил и моментов будут вызывать линейные и угловые ускорения.

Допустим, что самолет совершает неравномерный криволинейный полет в вертикальной плоскости. Центр тяжести его описывает кривую А – А (рис. 6) с центростремительным ускорением j_y и ускорением по траектории j_x. Самолет вращается при этом относительно оси Z, проходящей через центр тяжести, с угловым ускорением .

В первом приближении можно рассмотреть движение самолета по траектории как материальной точки с массой, равной массе самолета. Тогда уравнение движения в скоростной системе координат запишутся в виде:

.

Здесь g – ускорение свободного падения;

P,Q – подъемная сила и лобовое сопротивление;

α – угол атаки крыла;

β – угол наклона траектории.

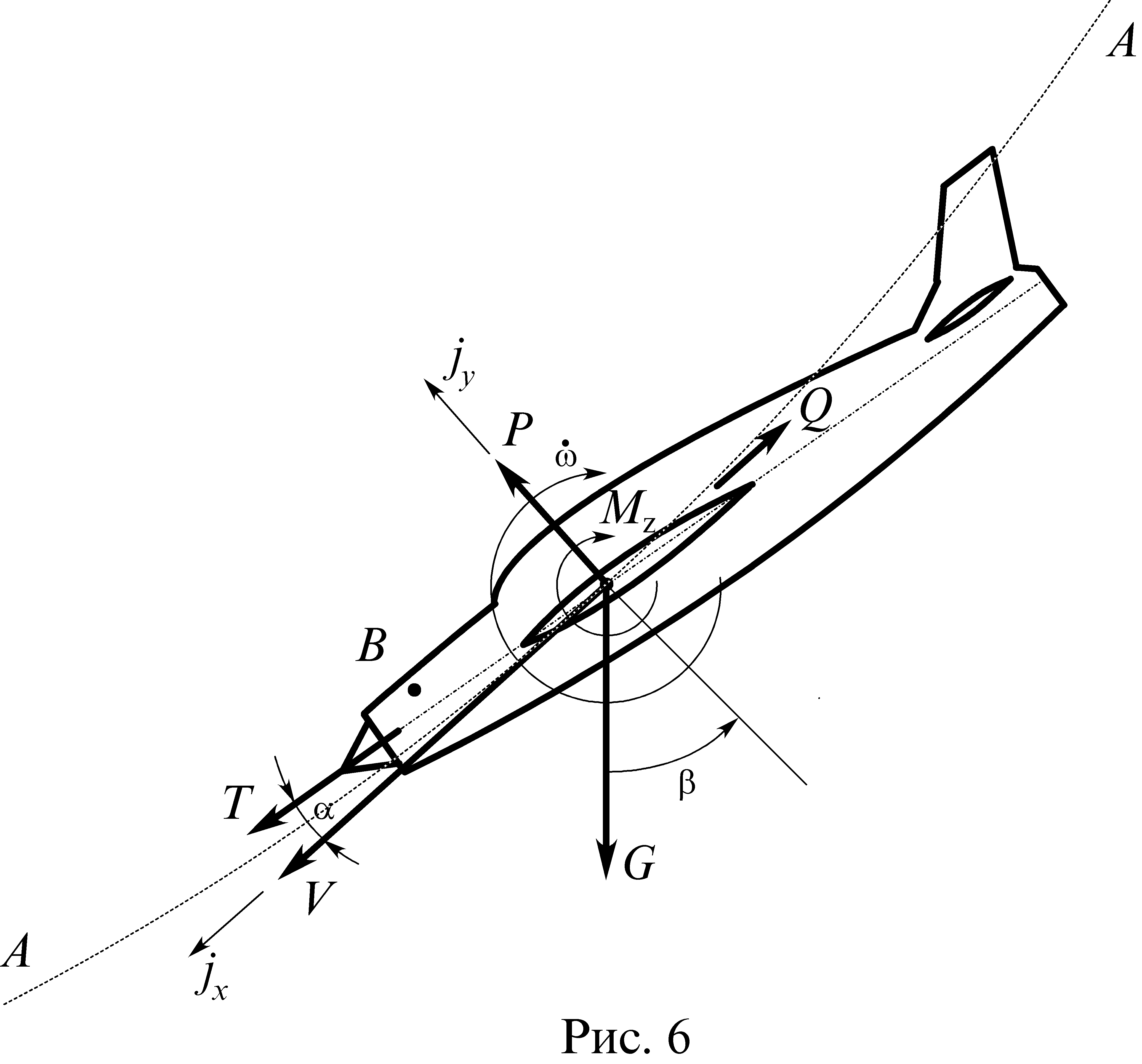
Указанные нагрузки рассматриваются в скоростной системе координат, в которой ось Х параллельна вектору скорости V. В связанной системе координат ось Х жестко связана с самолетом, т.е. связанные оси повернуты относительно скоростных на угол атаки α.

Если угол атаки считать малым, то sin α ≈ 0, cos α ≈ 1, различия между аэродинамическими силами в осях, связанных с самолетом и скоростных осях становятся несущественными и уравнения могут быть записаны так:

(1.2)

(1.3)

Известно, что центростремительное ускорение: ,

Где V – скорость по траетории;

r – радиус кривизны траетории.

Тангенциальное ускорение: .

Если в уравнениях (1.2) и (1.3) выделить члены, зависящие от веса самолета, и отнести их к его величине, получим:

(1.4)

(1.5)

Отношение внешних сил, действующих на самолет к его весу называется перегрузкой.

Рассматривая проекции сил на оси х и у получим перегрузки в направлении соответствующих осей:

; (1.6)

На основании первой из этих формул, перегрузка в направлении оси у определяется как отношение подъемной силы в криволинейном полете, к подъемной силе горизонтальном полете, т.к. она равна весу самолета.

Максимально возможная из перегрузок при совершении данного маневра, называется эксплуатационной перегрузкой.

Перегрузка характеризует маневренность самолета и позволяет достаточно просто определять массовые силы отдельных элементов конструкции.

Для иллюстрации приведем примерные значения максимальных эксплуатационных перегрузок некоторых типов самолетов:

7 – 9 – легкие маневренные самолеты

4 – 5 – легкие скоростные пассажирские

3 – 4 – средние пассажирские

2 – 3,5 – тяжелые пассажирские.

Следует отметить, что перегрузки на отдельные части самолета могут отличаться от рассмотренных. Дело в том, что мы рассматривали движение самолета как материальной точки. В действительности необходимо еще учесть вращение при движении по криволинейной траектории относительно центра масс с угловым ускорением (рис. 6). Тогда линейное ускорение точки В, расположенной близко к оси х, может быть записано так:

и значение перегрузки в точке В изменится на величину:

Кроме того, некоторая поправка должна быть внесена за счет упругих колебаний корпуса самолета и возникающих вследствие этого ускорений. Поэтому при экспериментальном изучении перегрузок весьма существенным оказывается вопрос о месте установки датчиков ускорений – акселерометров. Их следует располагать как можно ближе к центру тяжести самолета и в местах наименьших ускорений, вызванных упругими колебаниями.

Вопрос о нагрузках самолета является предметом обширных теоретических и экспериментальных исследований. Их цель – установить те условия, и режимы полета самолета, при которых возможно опасное нагружение для тех или иных агрегатов и узлов самолета.

Результаты этих исследований сводятся в специальный документ «Нормы прочности самолетов». Этим документом регламентируется величина, направление и характер распределения нагрузок на отдельные части самолета в различных условиях полета.

Режимы и условия полета, при которых возможны опасные нагружения отдельных частей или элементов конструкции самолета, называются расчетными случаями и обозначаются буквами.

Если для разных агрегатов расчетным является один и тот же случай, то он обозначается буквой с различными индексами.

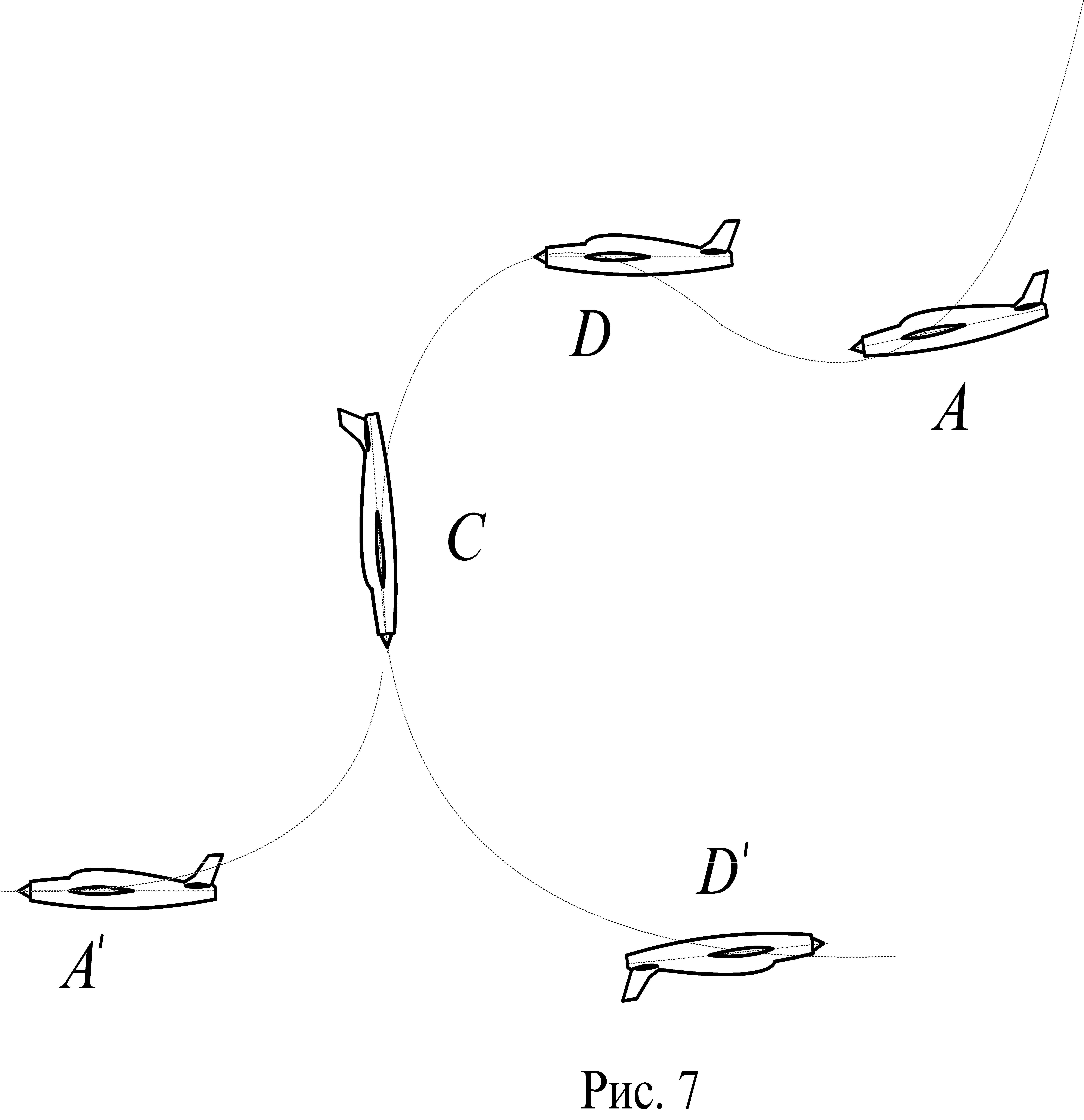
Примеры расчетных случаев (рис. 7):

Случай А’ – криволинейный полет в вертикальной плоскости на скорости, соответствующей максимальному скоростному напору q_{max max} пикирования или планирования.

Случай А – криволинейный полет в вертикальной плоскости при угле атаки, соответствующем максимальному коэффициенту подъемной силы С_умах.

Случай D – криволинейный полет в вертикальной плоскости на угле атаки крыла, соответствующем максимальной по абсолютной величине отрицательному коэффициенту подъемной силы (-С_у)_мах, с максимальной обратной перегрузкой.

Случай D’ – криволинейный полет в вертикальной плоскости на скорости, соответствующей 0,8 q_{max max}. Коэффициенты эксплуатационной перегрузки те же что и в случае D.

Случай С – пикирование с отклоненными элеронами на скорости, соответствующей q_{max max}. Подъемную силу крыла можно считать равной нулю. Рыло нагружено только значительными крутящими моментами.

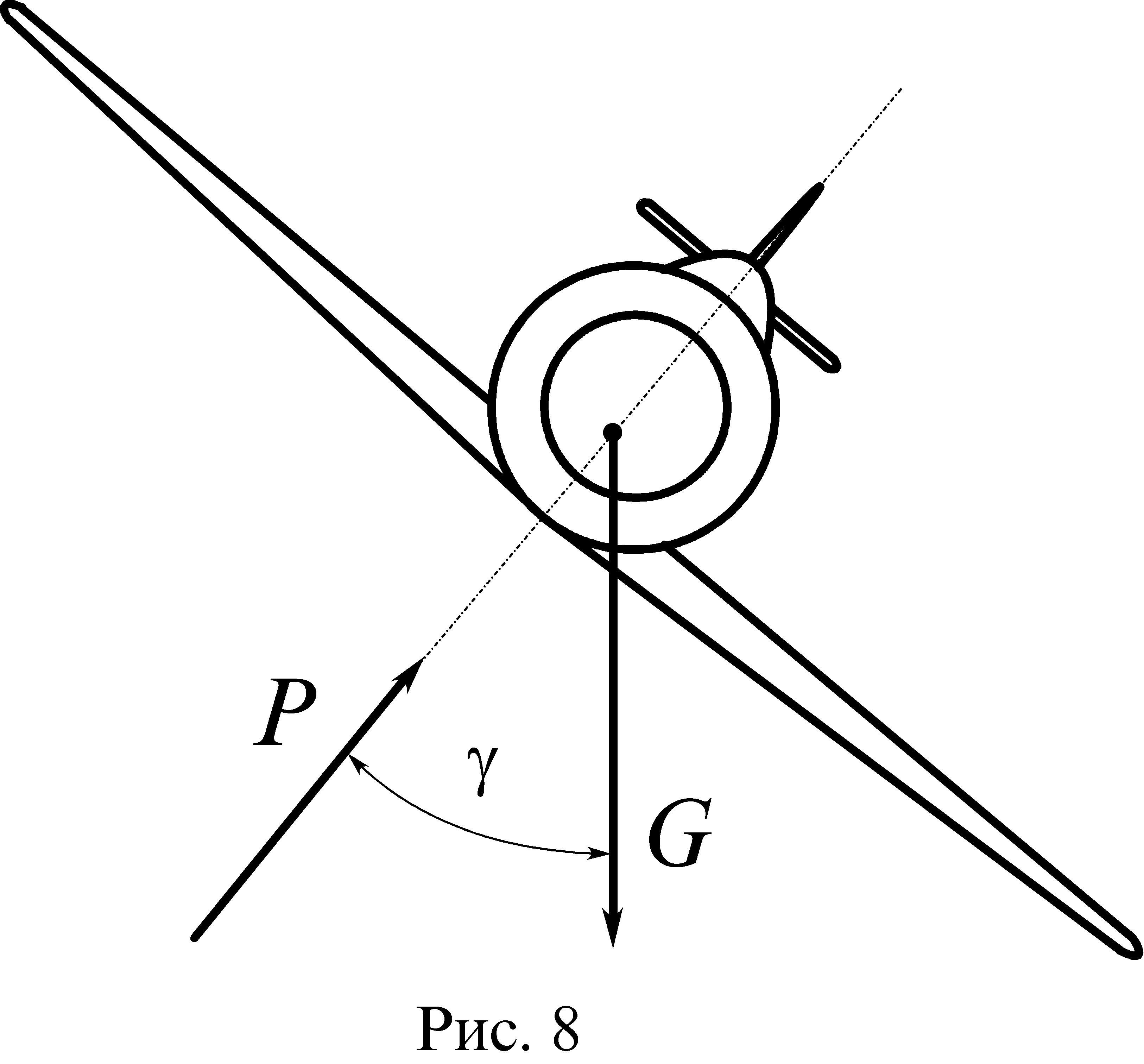
На рис. 8 схематично изображен самолет в состоянии виража без снижения. В этом случае вертикальные нагрузки самолета должны быть уравновешены, т.е.

Перегрузка для этого случая:

.

Перегрузки самолета возникают так же при встрече с потоком воздуха, имеющем некоторую скорость. Допустим, что самолет мгновенно из спокойной среды вошел в поток с вертикальной скоростью W (рис. 9).

Суммарная скорость набегающего потока будет в этом случае V ≈ V₀, т.к. V₀>>W, но угол атаки крыла увеличится на .

Следовательно, подъемная сила запишется так:

,

и поскольку ,

то перегрузка будет равна:

По каждому случаю нормами прочности совершенно точно задаются эксплуатационная нагрузка на соответствующие агрегаты самолета, ее направление и закон распределения по агрегату.